Inscription / Connexion Nouveau Sujet
Énergie mécanique ( un pendule)
Bonsoir
Bonne première nuit de 2016 , avec plaisir de vous présenter mes chers savants respectueux, mon centième TOPIC sur mon site préféré.
Alors , j'aurais besoin d'aide pour cet exercice.
Chapitre : énergie mécanique.
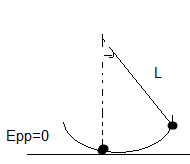
Un pendule simple est constitué d'un fil inextensible de longueur L= 1 m, de masse négligeable portant L'extrémité libre une masse ponctuelle m= 100g. Il est écarté de sa position d'équilibre d'un angle de 60 ° puis abandonné sans vitesse initiale.
1. Donner l'expression de l'énergie potentielle de pesanteur du pendule dans le champ de pesanteur lorsque le fil fait avec la verticale un angle
.
L'énergie potentielle est supposée nulle lorsque le pendule est en équilibre.
2. Compléter le tableau de valeurs ci-dessous en calculant l'énergie potentielle de pesanteur pour les valeurs données de l'angle .
| alpha (°) | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| Epp |
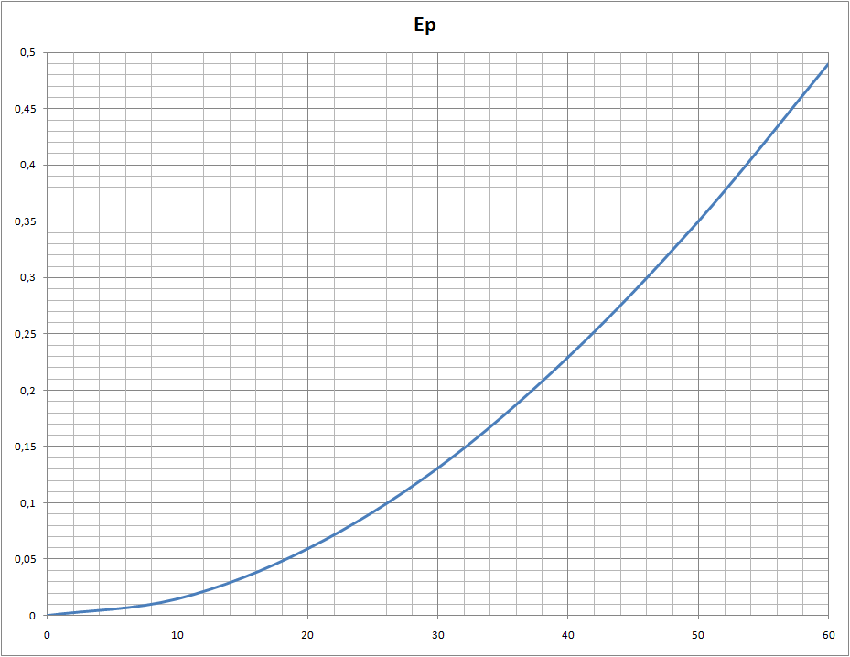
Tracer le graphe Epp (
)
3. Calculer l'énergie mécanique du pendule.
4. Donner l'expression de l'énergie cinétique Ec de la masse en fonction de
.
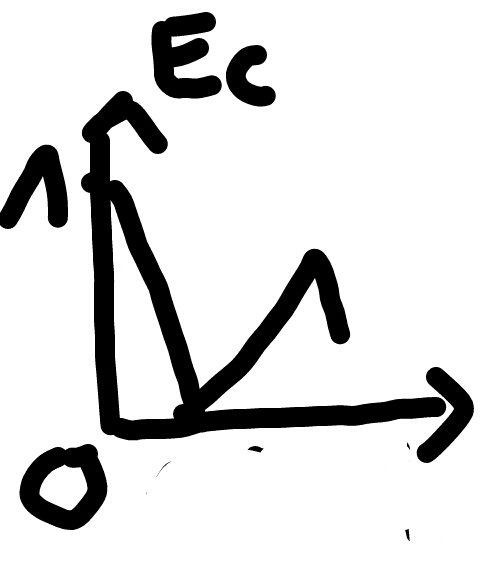
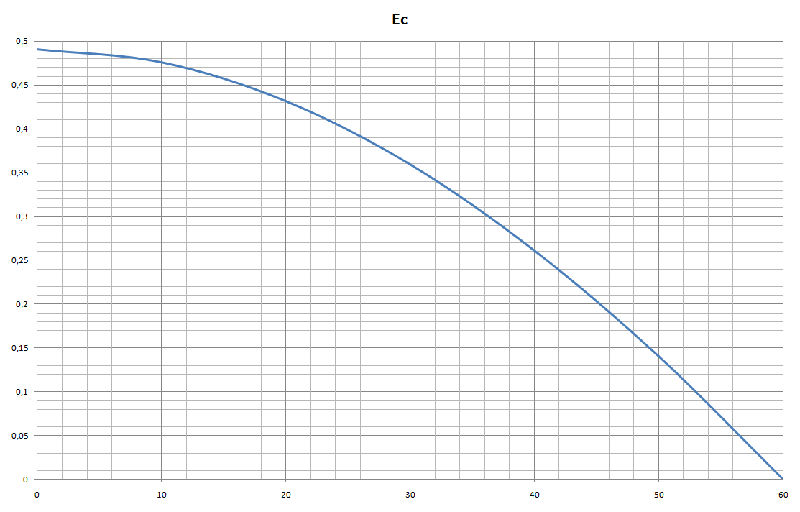
Tracer le graphe Ec (
).
5. Pour quelle valeur de
les énergies cinétique et potentielle sont - elles égales ?
Pour la question 1.
Epp= mgz , on peut continuer ?
Merci d'avance
Salut Aragorn
Ok , origine des attitudes:
Le point d'attache.
Donc Epp= mg(zi-zf)=(-Lcosi+Lcosf) ==>
Alpha= 0°
Epp=0
Alpha=10° ,
Epp= 0,48J
Alpha=20°,
Epp= 0,44J ainsi de suite
Mais ce que me fait etonner : c'est constater que Epp au lieu de diminuer elle augmente!
Ça Est-il correct ?
L'énergie potentielle est supposée nulle lorsque le pendule est en équilibre.
Donc :
0 0
10 0,015
20 0,059
60 0,49
Apparemment, je ne trouve pas la même chose que toi...
Il est normal que Ep augmente avec
(z augmente).Je ne trouve pas tout à fait la même chose mais tu as dû prendre g = 10 m.s-2.
Pour la courbe Epp, je suppose que ce n'est pas un problème.
Et pour la 3 ?
Salut Aragorn
Pour terminer:
3.
Le point où le pendule abandonné, Em= Ep=0,5J
4.
Le système se conserve alors:
Ec=Ep =mgL (1+cos)
Ainsi on a obtenu presque le même tableau, sauf si alpha=0°, Ec= 1J et si alpha= 60° imaginer que Ec= 0
5
Ec et Ep sont égales si alpha= 10 °, 20°,30°,40° et 50° ?
bonjours à tous.
3) la force qui travaille sur le pendule est conservative(le poids p)donc l'énergie mécanique est conservé :Em=Ec+Ep . En position =60°: Em=Ep.
4)Ec=Em-Ep.
5)Résoudre l'équation Ec=Ep de variable . Je vous laisse le soin de faire les applications numqs.
bon courage.
Bonjour à tous
Ok, je m'étais trompé pour 4.
Donc Ec= 0.5-mgL (1-cos)
Alors si alpha= 0, Ec= 0,5J
Si alpha= 60°, Ec=0
Ok Merci beaucoup Aragorn et Alhassan aussi
Au revoir
Pour la 3
On a : Em = Ec + Ep
Il y a un point où Ec = 0. C'est à l'élongation maximale ( = 60°).
Donc :
Pour la 4
On a toujours Em = Ec + Ep.
Donc :
On connaît Em (on vient de la calculer) et Ep.
Je vais tracer les courbes
Pour la 5
Il suffit de faire Ec = Ep
Il suffit de résoudre l'équation en cos
Annuler
connectez vous