Inscription / Connexion Nouveau Sujet
energie mécanique et moments de forces
salut , voici un problème oû je me suis bloquée
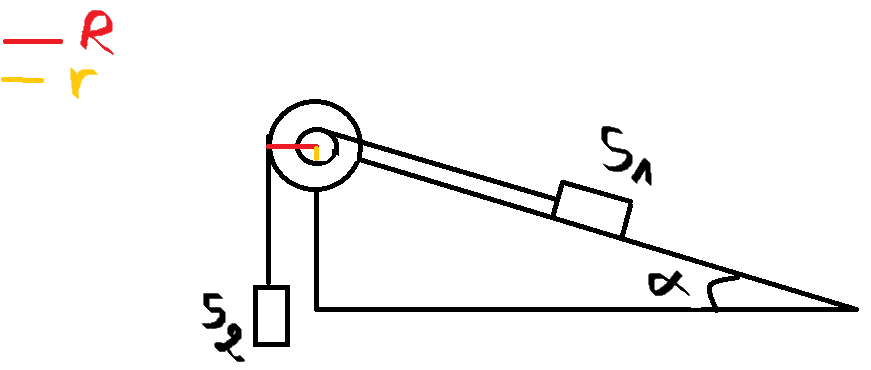
le système suivant est formé d'une poulie à deux gorges de rayon R=20cm et r=10cm, de deux solides m1 de masse S1et S2 de masse m2 et de deux fils inextensibles de masse négligeable capables de glisser sans frottement sur les gorges de la poulie . le coefficient de frottement sur le plan incliné est K=0.10
on donne :
g=10N/kg
m1=500g
J=1*10^-2 kg.m^2 le moment d inertie de la poulie
1) calculer la valeur minimale de la masse de S2 pour que s2 descend en bas
2) on prendra m2=m2(min) et on libère sans vitesse initiale le système ; calculer la vitesse V2 de S2 quand la poulie effectue deux tours
3) si on admet que les tensions des deux fils sont constantes au cours du mouvement calculer leurs intensités
deux fils inextensibles de masse négligeable capables de glisser sans frottement sur les gorges de la poulie . le coefficient de frottement sur le plan incliné est K=0.10
Hello
Il a l'air chouette ce dispositif ... mais tu peux nous le décrire un peu plus concrètemen?. 
Hum hum
calculer la valeur minimale de la masse de S2 pour que s2 descend en bas
C'est quoi s2? S1 en fait?
Si on augmente S2, la poulie aura plutôt tendance à entrainer S1 vers le haut... il me semble. A moins que je n'ai tjrs pas compris le dispositif ...
S2 est le corps qui va descendre en bas quand il va atteindre une certaine masse m2
minimale qui annuler l'équilibre et donc tirer S1 vers le haut
j'ai reçu une indication comme quoi pour calculer la masse minimale de S2 pour qu il descende en bas il faut que : le moment du poids de S2 soit plus grand que le moment de force de la tension du fils tenant le corps S1
Bon, on est d'accord qu'à partir d'une certaine valeur m2 de S2, le mobile S1 se retrouve entrainé vars le haut ...
Ce n'est plus ce qui était dans ton énoncé initial, mais tant mieux, c'est sans doute plus juste ...
Peux tu:
1) faire le bilan des forces pour les 2 systèmes suivants {S1}, {S2} et {Poulie}?
2) écrire la relation entre la force de frottement du support et la réaction de celui ci et déterminer ainsi une condition au déplacement de S1
3) Ecrire la somme des moments mécaniques en O pour le système {Poulie}
1)bilan des forces pour :
S1 : P1 le poids ; T1 la tension du fil ; F force de frottement ; Rn réaction normale du plan ; R' réaction de l axe de rotation
S2: P2 le poids ; T2 la tension du fil ; R'' réaction de l axe de rotation
poulie : P poids ; R réaction de l axe de rotation ; T1 ; T2
2)je n'ai pas compris ce que vous vouliez dire par condition de déplacement ??
pour le corps S1 :
en projetant le plan : Rn(y) + F(y) + T1(y) + P1(y) = 0
==> Rn-cos(alpha)xP1 =0
==> Rn = cos(alpha)xP1
on sait que k=f/Rn
==> f=kxRn
on remplace et on trouve F= kxcos(alpha)xP1=0,43N
3) la somme des moments mécaniques ??
R' réaction de l axe de rotation
R'' réaction de l axe de rotation
Je ne vois pas de quoi tu parles ...
condition de déplacement
vois dans ton cours la définition du coefficient de frottement ou bien du "cône de frottement"
tant que
somme des moments mécaniques ??
Calcule les moments des forces T1 et T2 en 0
A toi?
Zut, j'ai cliqué sur "poster"
il fallait lire ||\vec{F}|| <k.||\vec{N}|| et ||\vec{F}|| =k.||\vec{N}||
en faite je viens de trouver la réponse pour calculer la masse m2 minimale :
j'ai travaillé avec les conditions d'équilibre en S1 et S2 d'où j'ai trouvé l'expression de T1 et T2 puis j'ai résolu l'équation M(T2)=M(T1) et j'aii trouvé l'expression de m2 :
m2= m1(sin(alpha) + cos(alpha)xK) /2 = 146g
j'ai même trouvé l'expression de V2 qui est trop longue et l'écrire sur pc est difficile
je me suis bloquée sur la question 3 : le calcul des intensités des fils
Il est étrange que les rayons R et r ne ressortent pas de ton calcul de M(T1) et M(T2)
Peux tu les détailler?
on pose M(T2)=M(T1)
<==> m2 x g x R= m1 xgx(sin(alpha) +cos(alpha)xk)
<==> m2= m1[ sin(alpha) +cos(alpha)xk]xr le tout divisé par 2R
et puisque R= 20 cm et r =10 cm
donc R= 2r
==> m2 = m1(sin(alpha) + cos(alpha)xk)/2
Ok
C'est cette "manie " de mélanger expressions littérales et valeurs numériques ...
va pour le 1/2 qui passe pour le rapport r/R 
Tension des fils: l'énoncé dit que l'on admet qu'elles sont constantes durant le mouvement
Je te laisse donc réfléchir à ce que vaut le travail de T2 après les 2 tours de la question précédente ...
Annuler
connectez vous