Inscription / Connexion Nouveau Sujet
Energie mécanique
Bonsoir,
J'aimerais que vous m'aidez à traiter cette partie de mon sujet:
Exercice
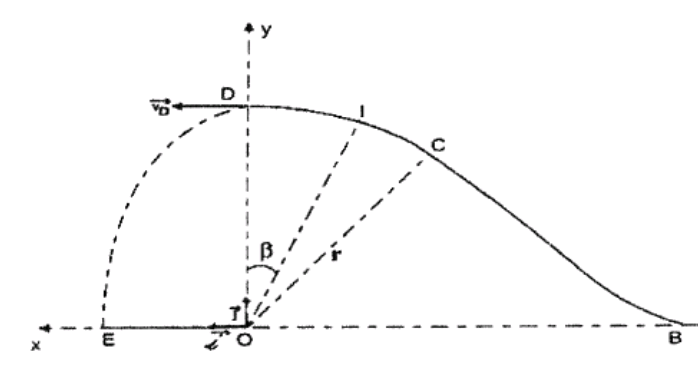
Sur la figure ci-dessous, CD est un arc de cercle de rayon r=75cm. Les frottements sont présents (uniquement) sur cette partie (CD) et équivalent à une force f (constante) colinéaire et de sens opposé à la vitesse de tout corps qui s'y déplace.
On lance une bille de masse m=100g avec une vitesse v=4m/s au niveau du point B. La bille arrive au point D avec une vitesse VD=0,75m/s.
On donne: g=10N/Kg ;la réference des énergies potentielles est le plan horizontal passant par E, O et B.
1)Calculer le travail de la force de frottement sur le tronçon circulaire CD.
Mon début:
La variation de l'énergie mécanique entre le point C et D est:
ΔEm=Em(D)-Em(C)=W(f)
Au niveau du point C, on deux énergies:
-l'énergie cinétique ½mV²c
-et l'énergie potentielle mgZc où Zc est l'altitude que je n'arrive pas à déterminer...car aucun angle précisé.
Au point D il y'a l'énergie cinétique : ½mV²(D) et l'énergie potentielle Ep(D)=mgr vu que OD=r...
Je n'arrive vraiment pas à déterminer W(f) sans Vc et Zc...
Auriez-vous une piste?
Em(D)-Em(C)=Ec(D)+Ep(D)-(Ec(B)+Ep(B))=W(f)
=>½mV²(D)+mgr-½mV²(B)=W(f)
=> W(f)=½*0,1*(0,75)²+0,1*10*0,75-½*0,1*4=0,58 J
Il faut justifier:
Em(D) - Em(B) = W(f) B->D = W(f) C->D
Car il ny a pas de frottement de B à C
Ensuite, une force de frottement est toujours dissipative donc son travail est toujours ....
Ton calcul est à revoir.


