Inscription / Connexion Nouveau Sujet
Énergie mécanique
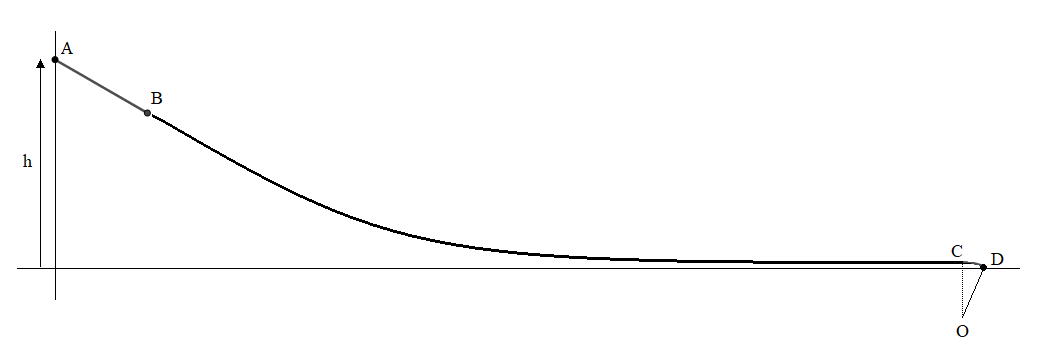
Salut à tous, voilà que je requiert de l'aide pour l'exercice suivant :Un enfant fais du toboggan sur une piste ABCD.la piste du toboggan de hauteur h=1,2m comprend trois portions AB,BC,CD.AB est rectiligne de longueur 40cm telle que 
=60°.CD est un arc de cercle de rayon r tel que r=20cm et l'angle COD=π\8.Les forces de frottements sont négligeables sur AB et BC polies et sont égales à une force unique de valeur 0,2N.L'enfant part du point A sans vitesse initiale.g=9,81N/kg. Questions: Détermine la vitesse de l'enfant :1-au point B,2-au point C,3-au point D. J'ai fais 1- . système : l'enfant . référentiel terrestre supposé galiléen . bilan des forces :_ le poids de l'enfant 
_la réaction du support 
. D'après le théorème de l'énergie cinétique sur AB,
Ec=
w(
avec W(vect R)=0J et EcA=0J car vA=0m/s donc 1/2mvB^2=W(vect P)
1/2mvB^2=mgh avec h=cos × AB alors vB=
2g(cos ×AB);AN:vB=2×10×cos 60°×0,4=√4=2m/s maintenant je peine à faire le 2 et le 3.Pourriez vous m'aider ?
Very, bonjour
tu as utilisé d'une drôle de manière certaines de nos balises
reprends ton texte, en le modifiant en conséquence, et fais aperçu avant d'envoyer pour vérifier que tout est bien lisible
n'hésite pas également à aérer un peu cet énoncé qui écrit ainsi ne donne pas trop envie
fais tout cela en réponse à mon message
merci
D'abord,je ne maîtrise pas bien les balises et puis pas besoin que je réécrive le texte,on peut s'en passer pour savoir de quoi il s'agit dans ce texte n'est ce pas ?
voilà ce qui est visible chez moi ...
tu n'as pas la même chose toi ?
Il y a un minimum de politesse vis à vis des personnes susceptibles de t'aider, et qui n'ont pas à reconstituer ton énoncé.
Ok voilà cette partie du texte corrigée: bilan des forces :le poids de l'enfant (vecteur P);la réaction du support (vecteur R).Ec=W(forces extérieures) avec W(vecteur R)=0J et Ec au point A=0J car la vitesse au point A notée vA =0m/s. W=travail
Bonjour,
Question 1:
Pour autant qu'on puisse s'y reconnaître dans le mélange indigeste "énoncé + propositions de réponses" j'ai cru comprendre que tu arrivais à la bonne relation donnant VB en fonction de g, AB, et α
En revanche, l'application numérique est à revoir puisque l'énoncé indique clairement que g = 9,81N/kg
Question 2 : Un schéma soigné remplacera avec profit le mauvais brouillon que tu as posté le 03-06-20 à 10:23
Ce schéma doit faire apparaître avec précision les limites de la hauteur "h" du toboggan et si le rayon OD est (ou n'est pas) horizontal
Ok,AN: VB=2×9,81(cos 60° × 0,4);VB=1,98m/s.A noter aucun défaut sur ce schéma,il est la copie conforme à l'original.Donc comme on peut le voir sur le schéma,le rayon OD n'est pas horizontal.
OK pour VB =1,98m/s
Puisque ton schéma est la copie conforme de l'original je me pose les questions suivantes sur cet original.
1) Sur le schéma le rayon OC semble vertical.
En est il bien ainsi ?
2) L'énoncé dit que la hauteur " h " du toboggan est de 1,20m ce que j'interprète comme étant la différence de niveau entre les points A et D ( ou bien entre A et O ? )
Pourtant le schéma montre la hauteur " h " comme étant la différence de niveau entre le point A et un point non visible sur le schéma mais situé nettement en dessous de D et un peu en dessous de O
Une autre manière de poser la question est de se demander pour quelle raison le niveau du sol n'est pas représenté car alors "h" représenterait la hauteur de A par rapport au sol.
Merci de préciser (ou de te faire préciser par ton professeur) ces deux points.
1)Oui,il est vertical;2) Comme dit auparavant le schéma est conforme à l'original,mais je pense que h égal à la différence de niveau entre A et D car au point D,il me semble que l'enfant touche le sol.Mais bon,si ce n'est pas le cas,serait il impossible de déterminer la vitesse au point C?
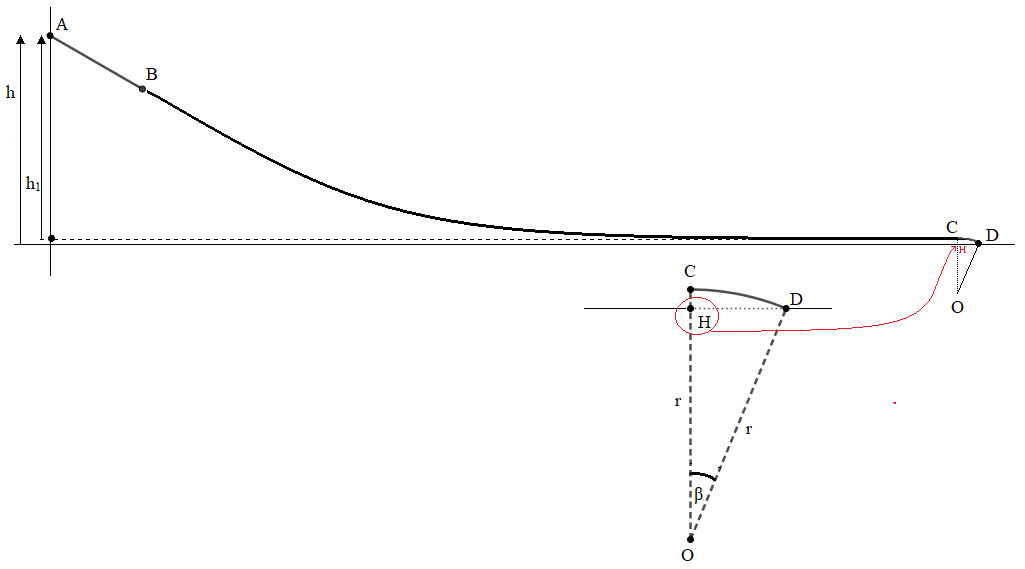
Ci dessous un schéma qui semble correspondre à ta description.
Question 2 :
Appliquer le théorème de l'énergie cinétique (ou la conservation de l'énergie mécanique) entre les points A et C
A propos du rayon, n'est il pas utile ici? Sinon le schéma proposé est acceptable, dommage que je ne puisse dessiner comme vous sur ce site 😒!
Je suppose que le rayon dont tu parles est celui de l'arc de cercle (CD)
Ce rayon ( r= OC = OD = 20 cm ) intervient dans le calcul de la dénivellation entre les points A et C
> Very
dommage que je ne puisse dessiner comme vous sur ce site ?!
mais si, tu peux ...
nous ne dessinons pas sur le site, nous dessinons dans un logiciel (geogebra ou autre peu importe), nous faisons une image, et c'est cette image que nous mettons sur le site
Oui.
Le terme de dénivellation signifie " différence de niveau ", le niveau étant lui même l'altitude par rapport à un plan horizontal de référence.
Ok,en appliquant le théorème de l'énergie cinétique, j'obtiens 1/2mvC^2=mgh1 avec h1=???. Sachant que h1 est la dénivellation entre A et C, h1 est-elle égale à h ? comment déterminer h1?
Ok,1/2mvC^2=mgh1 équivaut à vC^2=2gh1 ; AN:vC^2=2×9,81×(1,2-0,2(1-cosπ\8);vC^2=23,24 alors vC=√23,24;vC=4,82 m/s.Dans ce cas je peux faire la même chose pour déterminer la vitesse au point D avec la dénivellation entre les points A et D notée h2 et qui est égale à h.Merci pour votre aide !😁
Dans ce cas je peux faire la même chose pour déterminer la vitesse au point D avec la dénivellation entre les points A et D notée h2 et qui est égale à h.
Non, ce n'est pas aussi simple, car sur la portion CD s'exercent en plus du poids des forces de frottement (Voir énoncé)
Ok,en appliquant le théorème de l'énergie cinétique sur CD, j'obtiens EcD-EcC=W(vect P)+W(vect f) s'en suit 1/mvD^2-1/2mvC^2=mgh2+M (vecteur f)×
avec W: travail de force ;f: force de frottement ;M: moment de force et h2=CH.On a alors 1/2mvD^2-1/2mvC^2=mgh2 -f×OD × π\8 car le moment de f est le produit de sa valeur par le bras de levier qui est ici OD car la direction de f est tangente à l'arc de cercle CD.Donc vD^2={2(mgh2-f×OD×π\8+1/2mvC^2)}/m.AN:vD^2=[2{14×9,81×0,01-0,2×0,2×(3,14÷8)+0,5×14×23,24}]/14;vD^2=23,42m/s;vD=√23,42=4,84m/s.Désolé, j'avais oublié une donnée dans l'énoncé,la masse de l'enfant m=14kg
Je retiens de ce que tu as écrit que :
EcD-EcC=W(vect P)+W(vect f)
Ce qui est un bon point de départ.
Je n'ai pas la patience de déchiffrer la suite de ton texte qui est, à mon sens, confus et mal présenté.
Bonjour,
Dommage si vous n'avez pas la patience, pourtant je pense que j'ai trouvé
Ce n'est pas qu'une question de patience, c'est une question de respect des règles, de respect de celui qui prend le temps de t'aider et de préparation aux examens (bac, concours ...).
On t'a maintes fois rappelé la nécessité d'améliorer la qualité de tes sujets et de tes messages.
Voici un exemple de phrase qu'on trouve en amont d'un sujet de concours des écoles d'ingénieurs :
La présentation, la lisibilité, l'orthographe, la qualité de la rédaction, la clarté et la précision des raisonnements entreront pour une part importante dans l'appréciation des copies. En particulier, les résultats non justifiés ne seront pas pris en compte.
C'est aussi un motif d'avertissement et d'exclusion , ça aussi tu le sais ...
La prochaine fois ce ne sera pas qu'un simple rappel de la FAQ :
la FAQ du forum
remercier la personneBon après-midi
Attention à ce que tu proposes,tu dois plutôt diviser toute l'expression sous la racine par M, pas seulement 2fr.Et aussi à l'angle,tu as écris alors que tu avais auparavant noté l'angle π/8, .
Je maintiens l'expression de VD telle que l'ai écrite.
A partir de l'expression :
je multiplie les deux membres de l'égalité par (2/m) pour obtenir :
ce qui donne :
et par suite :
En revanche, il est vrai que j'ai changé par inattention la notation de l'angle COD que j'ai d'abord noté β puis ensuite θ
Oui,ça marche!et aussi multiplier le tout du deuxième membre par 2 et le diviser par m marche également tout en divisant le 1er membre par 1/2m à partir de l'expression de départ,ce que j'ai fais et tu n'as pris la peine de le lire .Fais maintenant l'application numérique et je suis certain que tu tomberas sur le même résultat que le mien .
Bonjour,
Fais maintenant l'application numérique et je suis certain que tu tomberas sur le même résultat que le mien
Very, tu n'inverses pas les rôles : c'est toi qui demande de l'aide et non l'inverse ... A toi de vérifier que tu retrouves le même résultat que celui d'odbugt1 si tu le souhaites, en guise de vérification ...
Annuler
connectez vous