Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

énergie mécanique.

Posté par
kamikaz 08-03-20 à 00:15

Bonjour,

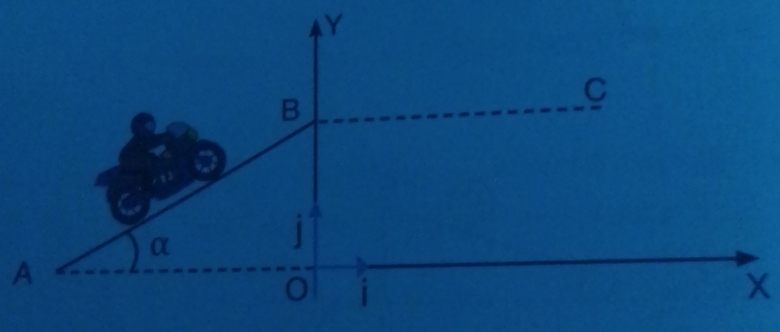
On décrit l'exploit du motocycliste Robbie Maddison .En effet le 31 Mars 2008 , l'Australien Robbie Maddison a battu son propre record de saut en longueur à moto sur un tremplin incliné d'un angle =27,0° par rapport à l'horizontale.Il a parcouru le tremplin AB avec une vitesse \vec{V} de valeur constante V=160km/h .Au point B, il s'est envolé pour un saut d'une portée BC=107m . Entre B et C , toute force autre que le poids est supposée négligeable.
énergie mécanique..

Données : g=9,81N/kg

, masse {motard+🏍️}=180kg

; AB=7,86m.

1) Donner l'expression de l'énergie mécanique du système {motard+🏍️+terre} en fonction de la vitesse v et de l'altitude y.

2) Calculer l'énergie cinétique du système au point A.

3)

3-1) Exprimer l'altitude YB du point B en fonction de AB et de l'angle .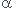

3-2) En déduire l'expression de la variation d'énergie potentielle de pesanteur du système, lorsqu'il passe du point A au point B.


3-3) Expliquer comment évolue l'énergie mécanique du système lorsqu'il passe de A à B . Justifier la réponse.

4)
4-1) Expliquer comment évolue l'énergie mécanique du système lorsqu'il passe de B à C . Justifier la réponse.

4-2) En déduire la vitesse du système au point C.

Posté par
diracre : énergie mécanique. 08-03-20 à 05:34

Hello

Et tu coinces à quel endroit?

Posté par
kamikazre : énergie mécanique. 08-03-20 à 08:09

Bonjour,

énergie mécanique..

Système : 🏍️+motard .

Référentiel : référentiel terrestre supposé galliléen

Bilan des forces :la réaction du support au plan incliné AB , le poids P sur le trajet AB.

Alors

1)EmAB=ECAB+EPAB

2) V=0 donc ECA=0J.

Or ECAB=1/2mV²AB et EPAB=mgy

D'où EmAB=1/2mV²AB+mgy

Posté par
kamikazre : énergie mécanique. 08-03-20 à 08:24

Je bloque à partir de 3)

Posté par
diracre : énergie mécanique. 08-03-20 à 18:01

1/ Em = Ec + Ep,p = \frac{1}{2}mV^2(M) + mg.y(M)

Si l'on fixe l'énergie potentielle nulle pour y(M) = 0

Donc

En A :   Em = \frac{1}{2}mV^2(A) + mg.y(A)
En B :   Em = \frac{1}{2}mV^2(B) + mg.y(B)
En C :   Em = \frac{1}{2}mV^2(C) + mg.y(C)

L'énoncé te dit que V(A) = V(B)  = 160 km/h  et laisse entendre que  y(B) = y(C)

Par ailleurs   y(B) - y(A) = \frac{AB}{sin\alpha}

Tu reprends le guidon?

Posté par
kamikazre : énergie mécanique. 09-03-20 à 07:27

Bonjour , merci .

Alors

1/ EmA=EmB=EmC

Donc l'énergie mécanique au total E=1/2mV²+m×AB/sin a.

Posté par
kamikazre : énergie mécanique. 09-03-20 à 07:34

Pourquoi YB-YA=AB/sin a ?

Posté par
diracre : énergie mécanique. 09-03-20 à 07:40

parce que j'ai regardé ton schéma

YA = YO

Et AOB est rectangle en O  donc \frac{OB}{AB} = sin\widehat{A} = sin\alpha

Posté par
kamikazre : énergie mécanique. 09-03-20 à 09:22

D'accord , si 07 h 27 est juste alors

2) comment faire ?

Posté par
diracre : énergie mécanique. 09-03-20 à 20:11

Citation :
2) comment faire ?


En A  Ec(A) = \frac{1}{2}mv(A)^2    avec, donné par l'énoncé,   v(A) = 160 km/h

Posté par
kamikazre : énergie mécanique. 09-03-20 à 20:36

Bonsoir , oui ça fait :

ECA=2304000J.

Posté par
kamikazre : énergie mécanique. 09-03-20 à 20:54

Alors 3) çà va faire YB=AB sin

Posté par
kamikazre : énergie mécanique. 09-03-20 à 20:54

Est ce juste ?

Posté par
diracre : énergie mécanique. 10-03-20 à 03:55

Ec(A) 178 kJ

Posté par
kamikazre : énergie mécanique. 10-03-20 à 07:34

D'accord donc

ECA=1/2 mVA²

Application numérique : m=180kg , VA=160km/s =400/9 m/s VA²=160000/81m²/s²

Alors EC=1600000/9=177777,7778≈177777,77J.

Posté par
kamikazre : énergie mécanique. 10-03-20 à 07:35

kamikaz @ 09-03-2020 à 20:54

Alors 3) çà va faire YB=AB sin
c'est juste ?

Posté par
diracre : énergie mécanique. 10-03-20 à 07:58

Citation :
EC=1600000/9=177777,7778≈177777,77J


je pense que tu pourrais songer à arrondir un peu plus: 0,1 J  c'est l'énergie cinétique d'une masse de 1 kg se déplaçant à 1,6 km/h. ici la moto a une de masse de 180 kg et se déplace à 160 km/h donc produire un résultat en kilo joule est pertinent

Si YB/AB = sin, on peut en effet conclure sans hésiter que YB = AB.sin

Posté par
kamikazre : énergie mécanique. 10-03-20 à 09:24

D'accord merci.

3-2) EPp=mg(ABsin a)

Posté par
kamikazre : énergie mécanique. 10-03-20 à 09:27

Comment faire 3-3) ?

Posté par
diracre : énergie mécanique. 10-03-20 à 18:57

3-2) en fait ce que tu appelles EPp est une variation d'énergie potentielle, il serai donc plus judicieux de la nommer Epp

Donc \Delta Ep_p = Ep_p(B) - Ep_p(A) = mgABsin\alpha

Em(A) = Ec(A) + Ep_p(A) = \frac{1}{2}mV^2(A) + Ep_p(A)
Em(B) = Ec(B) + Ep_p(B) = \frac{1}{2}mV^2(B) + Ep_p(B)

Avec V(B) = V(A) = V =160 km/h

Et \Delta Ep_p = Ep_p(B) - Ep_p(A) = mgABsin\alpha

Je te laisse donc conclure sur la variation (différence) d'énergie potentielle entre A et B

Posté par
kamikazre : énergie mécanique. 10-03-20 à 19:33

La variation de l'énergie potentielle ne se conserve pas donc ...

Posté par
diracre : énergie mécanique. 10-03-20 à 20:08

1/ je voulais écrire
"Je te laisse donc conclure sur la variation (différence) d'énergie mécanique entre A et B"

et non pas "Je te laisse donc conclure sur la variation (différence) d'énergie potentielle entre A et "B

2/ Ceci étant dit, ta phrase "La variation de l'énergie potentielle ne se conserve pas donc ..."
est maladroite: une chose (une énergie entre autre) dont on dit qu'elle se conserve (dans le temps, dans l'espace, ...) signifie que cette chose ne varie pas, donc écrire que la variation ne se conserve pas ... tu comprends que c'est troublant

Nous avions donc:

Em(A) = Ec(A) + Ep_p(A) = \frac{1}{2}mV^2(A) + Ep_p(A)   \\ Em(B) = Ec(B) + Ep_p(B) = \frac{1}{2}mV^2(B) + Ep_p(B)  

Avec V(B) = V(A) = V =160 km/h

Et \Delta Ep_p = Ep_p(B) - Ep_p(A) = mgABsin\alpha

Donc Em(B) - Em(A) = \Delta Ep_p = Ep_p(B) - Ep_p(A) = mgABsin\alpha > 0

L'énergie mécanique du système {moto+motard} augmente durant l'ascension de A à B

En effet, l'énergie cinétique du système restant constant entre A et B,
Il faut bien que la moto fournisse l'énergie correspondante à l'augmentation d'énergie potentielle associée à la montée en altitude du système  

Posté par
kamikazre : énergie mécanique. 10-03-20 à 20:25

D'accord merci beaucoup.

Alors donc 3-2) l'énergie potentielle de A à B augmente .

3-3) l'énergie mécanique du système lorsqu'il passe de A à B augmente car l'énergie potentielle de A à B augmente .

Posté par
kamikazre : énergie mécanique. 10-03-20 à 20:32

3-4) maintenant ...

Posté par
diracre : énergie mécanique. 10-03-20 à 20:49

Alors:

1/ il n'y as pas de 3-4)  dans l'énoncé

2/ Tu pourrais peut être bosser un petit peu plus  et cogiter ? sur le trajet A->B le moteur de la moto permet via le contact des roues avec le sol de conserver une vitesse/energie cinétique constante: c'est donc l'énergie fournie indirectement par le moteur qui va permettre l'augmentation de l'energie mécanique. Une fois atteint le point B, le moteur de la moto est sans effet puisque les roues tournent dans le vide, l'énergie mécanique va donc se conserver (aux frottements près, mais l'énoncé dit:"toute force autre que le poids est supposée négligeable. ")

Posté par
kamikazre : énergie mécanique. 10-03-20 à 21:29

D'accord merci beaucoup.

Posté par
kamikazre : énergie mécanique. 11-03-20 à 07:37

3-3) Expliquer comment évolue l'énergie mécanique du système lorsqu'il passe de A à B . Justifier la réponse. et calculer là .

Posté par
kamikazre : énergie mécanique. 11-03-20 à 07:41

Oups

kamikaz @ 11-03-2020 à 07:37

3-3) Expliquer comment évolue l'énergie mécanique du système lorsqu'il passe de A à B . Justifier la réponse. et calculer l'énergie potentielle .

Posté par
kamikazre : énergie mécanique. 11-03-20 à 07:53

Alors 3-3) l'énergie mécanique du système augmente lorsqu'il passe du point A au point B.

Alors ∆Epp=mgABsin

AN: m=180kg

g=9,81N/kg

Sin =sin27°

AB=7,86m=0,0786 cm


∆Epp=180×9,81×0,0786×sin 27°

=132,74J

∆EPp=132,74J.

Posté par
kamikazre : énergie mécanique. 11-03-20 à 08:02

4-1/ l'énergie mécanique du système lorsque le système passe de B à C se conserve car une fois atteint le point B, le moteur de la moto est sans effet puisque les roues tournent dans le vide .

4-2/ la vitesse au point C VC=0m/s .

Merci beaucoup.

Posté par
diracre : énergie mécanique. 12-03-20 à 04:40

Citation :
AB=7,86m=0,0786 cm


Les mètres c'étaient bien , ne surtout pas convertir, si on veut trouver des Joules à la fin. En passant 7,86 m = 786 cm = 0,00786 km

Citation :
4-2/ la vitesse au point C VC=0m/s .




L'énergie mécanique se conserve entre B et C:   Em(B) = Ec(B) +Epp(B) = Em(C) = Ec(C) + Epp(C)

L'altitude du point C étant la même que celle du point B:  Epp(C) = Epp(B)

Donc Ec(C) = Ec(B)

Don V(C) = V(B) = V(A) = V

Posté par
kamikazre : énergie mécanique. 13-03-20 à 14:48

Ok , merci beaucoup.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !