Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

énergie mécanique 2

Posté par
kamikaz 11-03-20 à 08:25

Bonjour ,

Merci par avance.

On remarque un wagonnet (W) d'un enfant . Le wagonnet de masse m=3kg , glisse à la vitesse V=5m/s sur un plan horizontal xx' parfaitement liste .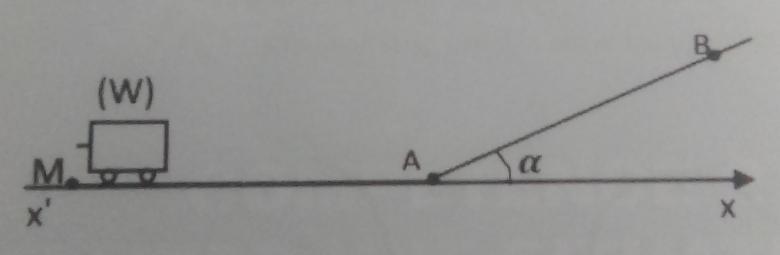énergie mécanique 2

Parti du point M , le wagonnet aborde au point A , une pente AB inclinée d'un angle =22° sur l'horizontale .Sur cette pente , il est soumis à une force de frottement d'intensité f=1,90N.
On veut étudier l'énergie mécanique de ce wagonnet lors de son déplacement.
L'énergie potentielle du wagonnet est considérée nulle lorsqu'il est en contact avec le plan horizontal x'x.
Donnée :g=9,8N/kg.

1) Donne l'expression de l'énergie cinétique.

EC=1/2mV²

2) Calculer l'énergie mécanique du wagonnet lorsqu'il se déplace entre x' et A.

3.

3-1) Déterminer la distance D parcourue par le wagonnet le long de AB avant de faire demi-tour.

3-2) Calculer la valeur de son énergie mécanique à cet instant.

4.

4-1) Déterminer la vitesse du wagonnet lorsqu'il repasse en A.

4-2) Calculer sa nouvelle énergie mécanique.

Posté par
odbugt1re : énergie mécanique 2 11-03-20 à 08:56

Bonjour,

Question 1 : OK

Question 2 : Il suffit de connaître et d'appliquer la définition de l'énergie mécanique.

Posté par
kamikazre : énergie mécanique 2 11-03-20 à 16:08

Ok

2) Em=Epp+Ec or ici Epp=0

D'où Em=1/2mV²=37,5 J...

3)1- j'ai du mal à déterminer AB puisse dans le triangle rectangle en x ,on ne connait aucune valeur ....

Posté par
odbugt1re : énergie mécanique 2 11-03-20 à 17:48

Question 2 :
Oui, entre M et A le wagonnet a une énergie mécanique qui est égale à son énergie cinétique laquelle est égale à 37,5J

Question 3.1 :
La longueur AB ne nous intéresse pas.
Le wagonnet s'arrête en un point C situé entre A et B
Ce qu'on cherche c'est la distance  D ( égale à AC )

Tu connais probablement le théorème de l'énergie cinétique.
C'est le moment de l'utiliser.

Posté par
kamikazre : énergie mécanique 2 11-03-20 à 18:31

je ne vois pas de AC .  

Posté par
kamikazre : énergie mécanique 2 11-03-20 à 18:32

Alors ∆EC=Ec2-Ec1...

Posté par
odbugt1re : énergie mécanique 2 11-03-20 à 18:54

Citation :

je ne vois pas de AC .  

L'énoncé dit que le wagonnet s'arrête sur la pente AB
Il ne dit pas qu'il s'arrête en B
Je décide donc de noter C ce point d'arrêt et comme on demande la distance D parcourue le long de AB avant l'arrêt je pose D =AC


Citation :
Alors ∆EC=Ec2-Ec1...

Enonce ce théorème clairement, cela permettra de l'appliquer !

Posté par
kamikazre : énergie mécanique 2 13-03-20 à 08:04

Bonjour ,

Alors 3-1) on a ∆ECAC=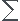 WAC(Fext)

ECC-ECA=-f×d or ECC=0 car Vc=0m/s ...

Alors -ECA=-f×d

ECA=f×d

\boxed{d=\dfrac{m×V_{A}²}{2f}}

d=\dfrac{3×25}{2×1,9}=19,73m

3-2)EmC=EPC+ECC or ECC=0J car Vc=0m/s

D'où EmC=EPC

Or EPC=mgh avec h= dsin ...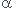

EPC=mgdsin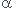

EPC=3×9,81×19,73sin22°=-5,14J

Donc EmC=-5,14J...

4-1) ECA=1/2mVA² or ECA=19,73×1,9=37,48J

Donc VA²=√(6,25)=2,50m/s ..

4-2) EmA=ECA

Donc EmA=1/2mVA²=1/2×3×2,5=3,75J...

Merci beaucoup.

Posté par
odbugt1re : énergie mécanique 2 13-03-20 à 10:20

On voit que tu as bien compris la démarche à employer.
L'ennui, c'est que tu n'as pas dressé l'inventaire des forces extérieures qui s'exercent sur le wagonnet.
Or le théorème de l'énergie cinétique dit :

"Dans un référentiel galiléen, la variation de l'énergie cinétique d'un solide est égale à la somme des travaux des forces extérieures appliquées pendant la durée de la variation."

Il en résulte que si ton raisonnement est globalement correct, tous les résultats sont faux.

Posté par
kamikazre : énergie mécanique 2 13-03-20 à 13:59

Oui , j'ai complétement oublié,

Alors

système :le wagonnet

Référentiel : référentiel terrestre supposé galliléen.

Bilan des forces : le poids , la réaction du support , la force de frottement.

Posté par
odbugt1re : énergie mécanique 2 13-03-20 à 14:53

Tu es sur la bonne voie ....

Posté par
kamikazre : énergie mécanique 2 13-03-20 à 23:06

Alors où est ce que mon calcul est faux ?

Posté par
odbugt1re : énergie mécanique 2 14-03-20 à 00:03

Il est faux parce que tu n'as tenu compte que de l'une des trois forces qui s'exercent sur le wagonnet.

E_C(C) - E_C(A) = W_{C \rightarrow A} (\overrightarrow{P}) +W_{C \rightarrow A} (\overrightarrow{R})+W_{C \rightarrow A} (\overrightarrow{f})

Posté par
kamikazre : énergie mécanique 2 14-03-20 à 07:28

D'accord , je vois maintenant .

Mais Rn =0 J non ?

Posté par
odbugt1re : énergie mécanique 2 14-03-20 à 08:38

Attention !
Dire que Rn = 0 est évidemment faux.
En revanche dire que W(\overrightarrow{R_n})=0 est exact puisque la réaction reste perpendiculaire au déplacement.

Posté par
kamikazre : énergie mécanique 2 16-03-20 à 22:45

D'accord .

Alors 3-1) système :le wagonnet

Référentiel : référentiel terrestre supposé galliléen.

Bilan des forces : le poids , la réaction du support , la force de frottement.

Application du théorème de l'énergie cinétique .

∆ECAC=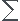 WAC(Fext)

ECC-ECA=-f×d or ECC=0 car Vc=0m/s ...

Alors -ECA=-f×d

ECA=f×d

\boxed{d=\dfrac{m×V_{A}²}{2f}}

d=\dfrac{3×25}{2×1,9}=19,73m

Posté par
kamikazre : énergie mécanique 2 16-03-20 à 22:46

Puisque W(Rn)=0J.

Posté par
odbugt1re : énergie mécanique 2 16-03-20 à 23:59

Tu as refait le même calcul que dans ton post du 13-03-20 à 08:04
Tu as donc trouvé le même résultat faux puisque tu as commis la même erreur en ne tenant pas compte du travail du poids.

Trois forces s'exercent sur le système. L'une des trois \vec{R_n} ne travaille pas, mais les deux autres \vec{f}~et~ \vec{P}travaillent.
Voir, si nécessaire, mon post du 14-03-20 à 00:03

Posté par
kamikazre : énergie mécanique 2 17-03-20 à 12:57

D'accord ,

Alors EC2-EC1=W(f) +W(P)+W(Rn) or \vec{Rn} \vec{AB} d'où W(En)=0J.

Donc EC2-ECa[/1ub]=W(f)+W(P/+0 or EC[sub]2=0J

D'où -1/2mV²=f×d +Psin 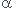×d.

-1/2mV²=d(f+Psin ).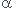

Donc d=-\dfrac{mV²}{2(f+Psin\alpha)}.

Application numérique.

m=3kg ,

V²=25m²/s²

f=1,9N

P=29,4N

Donc d=|-2,9|m=2,9m

D=2,9m.

Posté par
odbugt1re : énergie mécanique 2 17-03-20 à 15:49

Tu fais des "acrobaties" illicites à l'aide d'une valeur absolue pour éliminer un signe " - " qui te gène.
Au lieu de cette gymnastique douteuse il vaut mieux rechercher pour quelle raison tu trouves D = -2,9 m alors qu'à l'évidence le résultat doit être un nombre positif.

Ton erreur provient du calcul du travail de \vec f et de celui de \vec P
Ces deux forces sont des forces résistantes. Leurs travaux sont négatifs.

W_{A \rightarrow C} (\overrightarrow{f}) = - f * D \\ W_{A \rightarrow C} (\overrightarrow{P}) = - m * g * D * sin( \alpha )

En appliquant le théorème de l'énergie cinétique on obtient :

0 - (1/2) m (VA)² = - (f * D) - (m * g * D * sin()
ce qui conduit à

D=\dfrac{mV_A^2}{2~(f+m*g*sin(\alpha))}
D = 2,90m

Posté par
kamikazre : énergie mécanique 2 17-03-20 à 15:57

D'accord merci .

Alors

3-2) Em1--2=Ec 1--2+Epp1--2

Or Ec=1/2mV²=37,5J et Epp=mgsin D=31,94J

D'où Em1--2=69,44J.

Posté par
odbugt1re : énergie mécanique 2 17-03-20 à 16:39

Non

Citation :
3-2) Calculer la valeur de son énergie mécanique à cet instant.


" à cet instant " désigne, si j'ai bien compris l'énoncé l'instant où le wagonnet s'arrête pour faire demi-tour

Posté par
kamikazre : énergie mécanique 2 17-03-20 à 16:51

Oui , effectivement .

Alors Em=0J puisque Ec=0 J car V=0 et H=0 .

Posté par
odbugt1re : énergie mécanique 2 17-03-20 à 17:20

Non

Au moment où le wagonnet s'arrête pour faire demi-tour, son énergie cinétique est en effet nulle, mais pas son énergie potentielle de pesanteur.

Posté par
kamikazre : énergie mécanique 2 17-03-20 à 21:04

Oui , alors Em=Epp

Or Epp=mgsin =11,01J

D'où Em=11,01J.

Posté par
odbugt1re : énergie mécanique 2 17-03-20 à 23:03

Non.

EM(C) = Epp(C) = m * g * D * sin()

Posté par
kamikazre : énergie mécanique 2 18-03-20 à 11:16

Oui donc Em=31,93 J

4)

Posté par
odbugt1re : énergie mécanique 2 18-03-20 à 12:10

Oui

Si on prend soin de n'arrondir que le résultat final on obtient :
Em(C) = m * g * D * sin ()
Em(C) = 3 * 9,8 * 2,90395.... * sin (22°) = 31,98 J qu'on arrondit à 32,0 J

Le résultat final doit être arrondi, mais les résultats intermédiaires qui servent à l'obtenir ne doivent pas l'être.

Posté par
kamikazre : énergie mécanique 2 18-03-20 à 12:53

D'accord merci.

Comment faire pour 4) ?

Posté par
odbugt1re : énergie mécanique 2 18-03-20 à 14:51

Question 4 :
Même démarche que pour la question 3

Posté par
kamikazre : énergie mécanique 2 18-03-20 à 16:15

Oui mais le problème c'est que je ne comprends pas la question 4-1).

Posté par
odbugt1re : énergie mécanique 2 18-03-20 à 17:32

Ah bon ?
Il est pourtant difficile d'être plus clair.
Le wagonnet est déjà passé en A avec une vitesse V= 5m/s (voir énoncé)
Il a ensuite abordé la pente AB et s'est arrêté en C.
Il va maintenant redescendre et repasser en A avec une vitesse V'
On demande de calculer la valeur de V'

Posté par
kamikazre : énergie mécanique 2 19-03-20 à 20:56

Oui , c'est tellement simple .

Alors ∆EC1--2=-f×D-mgsin ×D

1/2mV2²-1/2mV1²=D(f+mgsin)

1/2mV2²=1/2mV1²+D(f+mgsin)


Est-ce que je suis sur la bonne voie ?

Posté par
kamikazre : énergie mécanique 2 19-03-20 à 20:58

Avec V' =V2...

Posté par
odbugt1re : énergie mécanique 2 19-03-20 à 23:38

Citation :
Alors ∆EC1--2=-f×D-mgsin ×D


Non.
Le poids est maintenant une force motrice : Son travail est positif
Le travail des forces de frottement reste négatif

(1/2) m (V'A)² - 0 = m * g * D * sin()  -  f * D

Posté par
kamikazre : énergie mécanique 2 21-03-20 à 16:42

D'accord , donc V'A= 2(Dgsin -f )

An : V'A²=-4,30m/s

bizarre ...

Posté par
odbugt1re : énergie mécanique 2 21-03-20 à 17:13

Plus que bizarre, c'est carrément impossible.

\dfrac{1}{2}*m*V_A^{'2}~=~m*g*D*sin(\alpha) -( f*D)

On multiplie les 2 membres de l'égalité par (2/m) :

V_A^{'2}~=~2*g*D*sin(\alpha)~-~ \dfrac{2*f*D}{m}

On factorise :

V_A^{'2}~=~2*D~\left (g*sin(\alpha) - \dfrac{f}{m}\right )

et on continue ....

Posté par
kamikazre : énergie mécanique 2 28-03-20 à 14:05

Citation :
On factorise :

V_A^{'2}~=~2*D~\left (g*sin(\alpha) - \dfrac{f}{m}\right )

et on continue ....

C'est encore impossible car

2×2,9(9,8×sin 22°-1,9/3)≈-4,18....

Posté par
odbugt1re : énergie mécanique 2 28-03-20 à 18:03

Puisque il faut tout te dire ....

V_A^{'2}~=~2*D~\left (g*sin(\alpha) - \dfrac{f}{m}\right )

V_A^{'2}~ = 2 * 2,9 * \left(9,8 * sin(22°) - \dfrac{1,90}{3}\right)

V_A^{'2}~=~5,8 * (3,67 - 0,63)~= 17,632

V_A'= \sqrt{17,632}  \approx 4,2m/s

Posté par
kamikazre : énergie mécanique 2 30-03-20 à 15:07

D'accord merci beaucoup.

Alors pour 4-2) EM=EC

Posté par
odbugt1re : énergie mécanique 2 30-03-20 à 15:13

Oui.

Posté par
kamikazre : énergie mécanique 2 30-03-20 à 15:15

Alors EM=1/2mV'A²

Donc EM=1/2×3×4,2²=26,46J.

Merci beaucoup.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !