Est-ce si difficile d'écrire un énoncé sans fautes et de mettre le dessin sur le site ?

Je le fais ... pour cette fois.

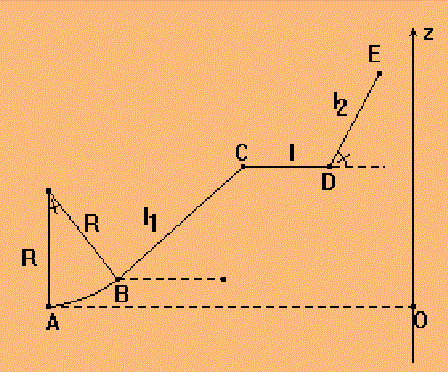
Dans un jeu de foire, on emporte le jambon si on envoie
en E un petit chariot se déplaçant sur un rail dont le profil
est représenté sur la figure.
AB est un arc de cercle de rayon R sous-tendant l'angle theta.
BC est une droite de longueur l1 incliné d'un angle alpha sur
l'horizontale, CD est un plan horizontal de longueur l,
DE est un plan de longueur l2 incliné d'un angle beta sur
l'horizontale.
1) Calculer les côtes de B, C, E ; A étant choisi pour
origine des côtes.
2) Quel est le travail du poids de l'objet quand il passe
de A à E ?
3) Quelle énergie cinétique minimale doit avoir le chariot lorsqu'il quitte A pour arriver en E ?
4) En réalité les frottements ne sont pas nuls. Dans l'intérêt du joueur (mais pas dans celui du forain) comment pourrait-on améliorer le profil du rail :
- en lui donnant un profil en arc de cercle de A en E ?
- en allongeant CD ou en le raccourcissant ?
- en lui donnant l'allure du plan incliné de A en E ?

D'abord avec tout mon respect à votre égard j'aimerai indiquer que je suis nouveau sur ce site , et puis j'avais un problème avec la figure qui ne voulait pas figurer parmi l'exercice. En plus je trouve votre réponse un peu"si je puis me permettre" brutal normalement ce site aide les personnes en physique chimie mais je pense que si l'on veut vraiment aider les gens on ne doit pas les vexer mais plutot les aider et les encourager, c'est là qu'on distingue le bon prof.  (avec tout mon respect). Sinon est-ce que quelqu'un aurait l'aimable volonté de m'aider svp ??

Ne pas arriver à mettre le dessin sur le site est une chose, ne pas relire ce qui a été écrit et corriger tout ce qui est incompréhensible en est une autre.

Mais comme tu n'apprécies pas mon style abrupt...  je m'abstiendrai de répondre plus avant.

Comme vous dites- Ne pas arriver à mettre le dessin sur le site est une chose, ne pas relire ce qui a été écrit et corriger tout ce qui est incompréhensible en est une autre-.
Mais c'est la façon de parler qui peut tout changer soit au mieux soit malheureusement au pire . J'ai effectivement pas relit mon exercice ni moins l'avoir corriger, je m'en excuse mais ce n'est pas une respectueuse façon de dire les choses donc svp si vous ne voulez pas m'aider rien ne vous y oblige. Et c'est bien effectivement là le problème que l'on rencontrait chez quelques profs autrefois mais heureusement que maintenant non ,enfin peut-être.

1)

A(0 ; 0)
B(R.sin(theta) ; R - R.cos(theta))
C(R.sin(theta) + L1.cos(alpha) ; R - R.cos(theta) + L1.sin(alpha))
...

L'ordonnée de E est :  R - R.cos(theta) + L1.sin(alpha) + L2.sin( Beta)

A comprendre avant de poursuivre.

Sauf distraction.

Merci
mais je n'ai pas bien compris pour la cote de B
Zb= R-R cos (theta)
.pour les autres c simple .
et merci.

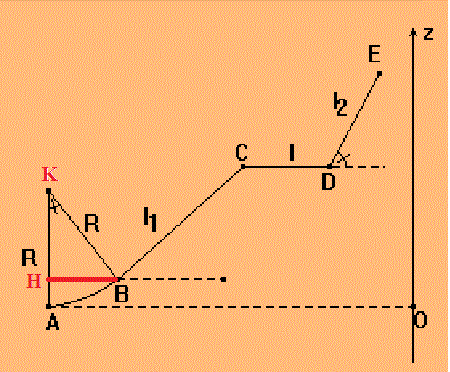
Dans le triangle BHK :

KH = KB.cos(HKB)
KH = R * cos(theta)

Or KA = HA + KH
--> R = HA + R * cos(theta)
HA = R - R * cos(theta)

H est à la même "altitude que B et donc z(B) = HA = R - R * cos(theta)

Ah d'accord j'ai compris ce point merci bcp

Sinon pour le travail il sera négatif car ici le travail du poids est résistant
W(p) = - m g Ze???? non

Oui.  

et svp pour la 3 ème question je n'ai pas bien saisi:)

3)

Il faut que : l'énergie cinétique en A + travail du poids sur (AE) >= 0

Ec - mg.zE >= 0
Ec >= mg.zE

Donc Ec minimum en A = mg.zE

Avec cette énergie cinétique en A, le mobile arrivera en E juste à vitesse nulle.

Cela, c'est si il n'y a aucune perte par frottement sur le trajet AE
-----
4)

Si il y a des pertes par frottement, alors pour atteindre le point E, il faudra que l'énergie cinétique du mobile en A soit plus grande que mg.zE

Pour "aider" le joueur, il y a donc intérêt à diminuer les pertes par frottement.

Il reste donc à réfléchir sur les stratégies possibles pour y arriver...

pour question 3
peut-on dire d'après le théorème de variation de l'énergie cinétique E_c= (F_exterieure)
  puisqu'il n'y a que le poids du corps donc E_c=mg Ze
  puisqu'elle est toujours positive ??????????????

pour 4
est ce qu'on peut dire en allongeant la partie CD ?????
       ET REMERCI
    

Modifier la longueur CD ... OUI mais encore ?

On peut présumer que l'auteur à voulu écrire modifier la longeur de CD MAIS en laissant les points B et D aux mêmes endroits (sinon cela n'aurait guère de sens)

Par exemple, modifier le chemin en rouge pour le transformer en un chemin comme le bleu.

Ce n'est pas précisé non plus dans l'énoncé, mais quel est est le type de frottement ? On peut présummer que c'est du frottement sec (le plus probable) ... mais alors :

La force de frottement n'est pas constante, elle dépend du coefficient de frottement (µ) piste-mobile et de la composante normale (N) de la réaction de la piste.

Donc pour la partie CD :

N = P * cos(alpha) et donc f = - µ * P * cos(alpha)
BC = h.sin(alpha)

Le travail de la force de frottement sur le trajet BC est donc : Wf1 = - f * BC = - µ * P * h * cos(alpha) * sin(alpha)
Le travail de la force de frottement sur le trajet CD est Wf2 = - P * µ * L (avec L = CD)

Le travail de la force de frottement sur le trajet rouge est donc : Wf = - µ * P * h * cos(alpha) * sin(alpha) - P * µ * L
-----
Soit alpha' l'angle entre l'horizontale et BN

N = P * cos(alpha') et donc f = - µ * P * cos(alpha')
BN = h.sin(alpha')

Le travail de la force de frottement sur le trajet BN est donc: Wf1' = - f * BN = - µ * P * h * cos(alpha') * sin(alpha')

ND = CD - CN
Avec CN = BN.cos(alpha') - BC.cos(alpha)
ND = L - (BN.cos(alpha') - BC.cos(alpha))
ND = L - (h.sin(alpha').cos(alpha') - h.sin(alpha).cos(alpha)) = L - h.sin(alpha').cos(alpha') + h.sin(alpha).cos(alpha)

Le travail de la force de frottement sur le trajet ND est Wf2' = - P * µ * [L - h.sin(alpha').cos(alpha') + h.sin(alpha).cos(alpha]

Le travail de la force de frottement sur le trajet bleu est donc : Wf' = - µ * P * h * cos(alpha') * sin(alpha')  - P * µ * [L - h.sin(alpha').cos(alpha') + h.sin(alpha).cos(alpha]

et en simplifiant ...

Wf' = - P * µ * [L + h.sin(alpha).cos(alpha))]

Le travail de la force de frottement sur le trajet bleu est donc : Wf' = - P * µ * [L - h.sin(alpha).cos(alpha))]
-----
Et on s'aperçoit que Wf = Wf'

Donc modifier la longueur du palier CD (en conservant bien entendu les positions de B et D), n'a pas d'influence sur le travail de la force de frottement... dans le cas d'un frottement sec.

Mais je ne suis pas sûr que cela soit du niveau 1ere ... et je reste aussi méfiant sur l'interprétation de celui qui a rédigé cet exercice... s'il a considéré (à tort) la force de frottement comme constante alors les conclusions sont différentes.

Sauf distraction.  

wow je pense que c un niveau un plus élevé pour  quelqu'un en première
et merci de m'avoir aidez tout au long de cet exercice