Inscription / Connexion Nouveau Sujet
Energie cinétique et Pendule.
Bonjour
, J'ai un problème sur cette exo.
Pouvez vous m'aider SVP ?
Un pendule avec un fil de longueur L=1.0m, de masse négligeable et une bille de masse m=100g.
Après avoir écarté d'un angle 
=45° , on lâche le pendule sans vitesse initiale.
Lorsqu'il passe à la verticale, il rencontre un clou situé a mi-longueur du fil. Négliger les frottements.
1/ Faire le BDF exercé sur la boule.
J'ai mis : P ( poids) et T ( tension du fil)
2/Sans calculer , dire quelles sont les forces qui travaillent.
Seulement P travaille car T est perpendiculaire.
3/Quelle est la valeur maximale que peut atteindre l'angle 
?
Je ne sais pas comment faire.
4/Si on divise pas deux l'angle initial quelle est la nouvelle valeur de ?
Idem que pour la 3/.
5/Quels sont les transformations d'énergie au cours des deux phases du mouvement?Quelle est la force responsable du transfert ?
Je pense que c'est a cause du clou.La force responsable est T.
6/ Calculer pour =45° , la vitesse de la boule quand la pendule passe a la verticale.
J'ai utilisé cette formule. m.g.h = (1/2).m.v²
Pour la 3/ j'ai éssayé ça:
VB²-VA² = 2.g.l.(1-cos)
Sachant que VA²=0 car "on lâche le pendule sans vitesse initiale."
On a: VB² = 2.g.l.(1-cos)
J'ai trouvé 5.74
Je ne sais pas si la réponse est correcte.
2)
Tu écris T est perpendiculaire.
Mais si tu ne dis pas perpendiculaire à quoi, cela ne veut rien dire.
---
3)
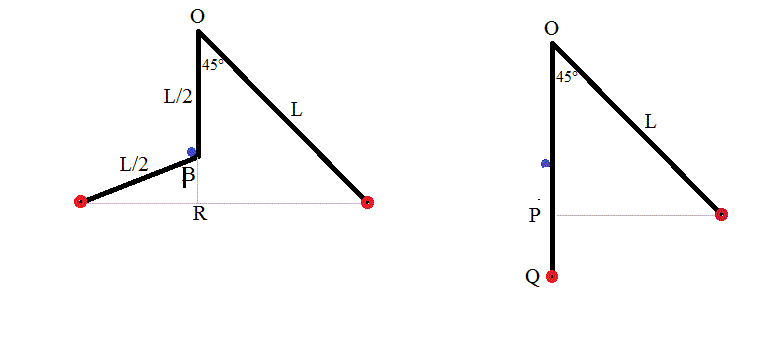
En supposant que Beta est l'angle de mon dessin. (dessin de gauche)
La masse remontera à la même altitude que celle de l'endroit où elle a été lachée au début.
OR = L.cos(45°) = L/V2 (avec V pour racine carrée)
BR = OR - L/2
BR = L/V2 - L/2
BR = (L/2).cos(beta)
L/V2 - L/2 = (L/2).cos(beta)
(2/L).(L/V2 - L/2) = cos(beta)
2.(1/V2 - 1/2) = cos(beta)
(V2 - 1) = cos(beta)
beta = 65,5°
---
4)
Calcul analogue à la 3 mais avec alpha = 22,5°
...
---
6)
Dessin de droite :
OP = L.cos(45°)
PQ = OQ - OP
PQ = L - L.cos(45°)
PQ = L.(1 - cos(45°))
Avec L = 1 m : PQ = 1*(1-cos(45°)) = (1 - (1/V2)) m
Avec V1 la vitesse au passage de la masse en Q :
(1/2).m.V1² = m.g.PQ
V1² = 2.g.PQ
V1² = 2 * 9,81 * (1 - (1/V2))
V1 = 2,4 m/s
---
Sauf distraction.
Annuler
connectez vous