Inscription / Connexion Nouveau Sujet
énergie cinétique, énergie potentielle élastique
Bonjour,
J'ai un exercice sur lequel je réfléchis depuis 2 jours. Je comprends la première question mais je ne sais pas comment commencer. Merci de m'aider !
Voici l'énoncé:
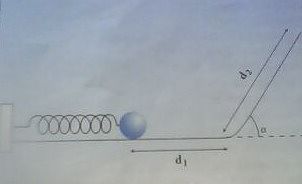
Un ressort élastique de raideur k peut être comprimé. Un dispositif convenable permet de le libérer, et le ressort propulse ainsi une bille parfaitement sphérique de rayon r= 2cm, de masse m= 100g, qui roule sans glisser sur le support.
La bille, après séparation du ressort, parcours la distance d1= 20 cm sur le plan horizontal. Ensuite, elle aborde un plan incliné d'un angle α= 30° par rapport au plan horizontal. Elle parcourt une distance d2 sur le plan incliné, puis rebrousse chemin.
On suppose les frottements négligeables sur le plan horizontal et sur le plan incliné.
1) Sachant que le raccourcissement x du ressort est proportionnel à la force F exercée par l'opérateur. Calculer k si F= 2 N ET x= 10 cm.
Quel est le travail effectué par l'opérateur pour raccourcir ainsi le ressort ?
2)Le ressort comprimé est libéré. Quel est, au départ, l'énergie cinétique de la bille ?
Quelle est l'énergie cinétique au moment où elle termine son trajet sur le plan horizontal ?
3) Quelle distance d2 parcourt la bille sur le plan incliné avant de rebrousser chemin ? On prendra g= 10 N.kg-1.
4) Quelle était la vitesse angulaire de la bille après un parcours d'2=10 cm sur le plan incliné ?
On rappelle qu le moment d'inertie d'une sphère par rapport à un axe de rotation passant par son centre a pour expression : JΔ= 2/5 mr².

pour la question numero 1, on sait que T=kx or = -
donc T=F=kx tu tires maintenant k.bon je crois que ça t'aidera pour la suite


sache également que durant tout le trajet horizontal c'est l'energie mecanique que tu utiliseras exemple:
pour la 2 question
soit x0 l' abscisse du ressort à vide et x1 l'abscisse du ressort en compression tel que x1= -10cm et x'0 l'absisse ou il repasse par x0
Em1= E'm0
Epe1 = E'c0
tu n'as qu'a calculer Epe1 pour determiner l'energie cinetique acquise quand il passe par l'origine
bon j'espère avoir été coherent
1)
|F| = k|x|
2 = k * 0,1
k = 20 N/m
W = (1/2).k.x² = (1/2) * 20 * (0,1)² = 0,1 J
-----
2)
Ec bille au départ = 0 (puisque vitesse nulle)
Ec bille au moment où elle termine son trajet sur le plan horizontal : 0,1 J mais dont une part en energie cinétique de translation et une part en énergie cinétique de rotation.
-----
3)
Au moment où la bille rebroussse chemin, sa vitesse est nulle et son son énergie cinétique aussi, l'énergie de la bille est donc uniquement sous forme potentielle de pesanteur.
A ce moment, on a donc: mgd2.sin(alpha) = 0,1 (puisqu'il les effets de frottement sont négligé).
mgd2.sin(alpha) = 0,1
0,1 * 10 * d2.sin(30°) = 0,1
d2 = 0,2 m
-----
4)
Ecinétique de la bille après un parcours d'2=10 cm sur le plan incliné : Ec2 = 0,1 - mgd'2.sin(alpha) = 0,1 - 0,1 * 10 * 0,1 * sin(30°) = 0,05 J (une partie en énergie cinétique de translation et une partie
en énergie cinétique de rotation).
Soit v la vitesse de translation de la bille à ce moment, on a w = v²/r la vitesse de rotation de la bille autour d'un axe passant par son centre, r est le rayon de la bille
Ec de translation = (1/2).mv² = (1/2).m.w².r²
Ec de rotation = (1/2).J.w² = (1/2)*(2/5).m.r².w² = (1/5).m.w²r²
Ec totale = (1/2).m.w².r² + (1/5).m.w²r² = 0,7.m.w².r².
0,7.m.w².r² = 0,05
0,7 * 0,1 * w² * 0,02² = 0,05
w = 42 rad/s (arrondi à 2 chiffres significatifs).
-----
Sauf distraction. Vérifie les calculs 


