Inscription / Connexion Nouveau Sujet
Énergie cinétique de N°6
Bonjour
J'aurais besoin d'aide pour cet exercice :
Chapitre : énergie cinétique.
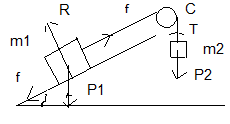
On considère le dispositif ci-dessous:
Les deux masses m1 et m2 sont identiques m1=m2= 1kg
-AB est un plan incliné ( =30°)
=30°)
-(C) est une poulie de masse négligeable.
-(f) est un fil inextensible de masse négligeable.
Les forces de frottement entre le plan incliné et la masse m1 sont équivalentes à une force unique en sens contraire du déplacement.
Le système est abandonné sans vitesse, la masse m2 se trouvant à une hauteur h=80 cm du sol.
1. Calculer la vitesse de la masse m2 au moment où elle arrive au sol.
2. Quelle est la distance parcourue par la masse m1 avant de s' immobilier sur le plan AB et de faire demi-tour ?
On donne f= 2 N
Mes réponses :
1.
Système: la masse 2
BFA: P2, T
TEC: Ecf-Eci = W (Fext)
W (Fext)
1/2 m2V ^ 2= m2gh+T.h
Or T=P <==>
V2= 35,77 m/s ?
Merci d'avance 
Re-salut.
Tout est à revoir dans votre étude.
Vous faites une erreur majeure en écrivant pour le solide 2 : T = P, si cela était, on aurait càd un mouvement rectiligne uniforme ou un équilibre puisque l'ensemble du dispositif est abandonné sans vitesse initiale.
Quelques pistes pour avancer...
Le théorème de l'énergie cinétique est une bonne technique de résolution.
Etudiez le système dans son ensemble : {S1, S2, poulie, fil}, le fil étant inextensible, les deux solides auront même vitesse v et les tensions de fil deviendront des forces intérieures dont vous n'aurez plus à vous préoccuper. Les seules forces effectuant des travaux seront la force de frottement qui s'exerce sur S1 et les poids de chacun des DEUX solides (attention, l'un sera moteur, l'autre résistant).
Bon, j'en ai assez dit, à vous de jouer.
1)
Force motrice : F = m2.g - m1.g.sin(alpha) - f
F = (m1+m2)*a (car la masse de la poulie est négligée et donc aussi l'effet de son moment d'inertie)
m2.g - m1.g.sin(alpha) - f = (m1+m2)*a
1 * 10 - 1 * 10 * sin(30°) - 2 = (1+1) * a
a = 1,5 m/s² (accélération des masses).
---
h = at²/2
v = a.t
0,8 = 1,5*t²/2 --> t = 1,0328 s
v = 1,5 * 1,0328 = 1,55 m/s (vitesse de la masse m2 à l'arrivée au sol)
-----
Autrement :
Travail du poids de (masse m2) sur la descente : W1 = m1.g.h = 1 * 10 * 0,8 = 8 J
Travail du poids de (masse m2) sur la montée (jusqu'à ce que m2 arrive au sol): W2 = - m2.g.h*sin(alpha) = - 1 * 10 * 0,8 * sin(30°) = - 4 J
Travail de la force de frottement : W = -2 * 0,8 = -1,6 J
W1 + W2 + W3 = (1/2).(m1+m2).v²
8 - 4 - 1,6 = 1/2 * (1+1) * v²
v = 1,55 m/s (vitesse de la masse m2 à l'arrivée au sol)
-----
2)
Energie cinétique de m1 au moment où m2 touche le sol : Ec = 1/2.m1.v² = 1,2 J
Soit d la distance que m2 continuera à avancer sur le plan incliné, on a:
(m2.g.sin(alpha) + f) * d = 1,2
(5 + 2) * d = 1,2
d = 1,2/7 = 0,17 m
Donc depuis le début (laché de m2), le masse m2 a avancé de 0,8 + 0,17 = 0,97 m sur le plan incliné.
La masse m2 va ensuite faire demi tour puisque tirée vers la bas du plan incliné par une force F' = m1*g*sin(alpha) - f = 1 * 10 * sin(30°) - 2 = 3 N
La résultante des forces sur la masse m2 est alors de 3 N dirigés suivant la direction du plan et dans le sens de la descente... la masse m2 redescend.
-----
Sauf distraction (rien relu) 
Salut J-P
Parfait , tout est joli
mais je ne vois pas d'où viennent ces expressions suivantes?:
Q2
(m2.g.sin(alpha) + f) * d
m1*g*sin(alpha) - f
Merci
----------
Merci aussi Picard pour vos explications, elles sont très intéressantes
Je sais pas pourquoi
W (P2)= -mgh*sin (alpha)
Je pense que il y a une confusion entre les indices 1 et 2 sur les masses m1 et m2 ?
Merci de m'expliquer 
Travail du poids de (masse m1) sur la montée (jusqu'à ce que m2 arrive au sol): W = - m1.g.h*sin(alpha) (j'ai noté ce travail W2 ... mais ne pas le confondre avec W(P2) ... que moi j'ai noté W1)
La masse m1 monte, donc le travail de son poids est négatif.
Ce travail vaut m1*g*H avec H la différence d'altitude entre le départ et l'instant considéré.
m1 a avancé sur le plan incliné de h = 0,8 m (puisque la corde est de longueur constante), cela correspond à une différence d'altitude H = h * sin(alpha)
---> W = - m1.g.h * sin(alpha)

---> W = - m1.g.h * sin(alpha)
Je n'avais pas su la différence d'altitude
Pourriez vous m' expliquer cela ?
Merci

Autre question
Pourquoi la somme des deux masses m1+ m2 dans l'énergie cinétique finale?:
1/2. (m1+m2)V2
Je concentre sur la dernière méthode parce que je pense que c'est plus compréhensible en mon niveau
Alors j'ai passé un grand temps pour essayer de comprendre
je sais que votre méthode est très délicate et intelligente
Mais je n'arrive même pas à comprendre certaines expressions posées
Comme celle de (m2.g.sin (alpha)+f)*d:
Je me suis dit qu'elle pourrait venir de P1*(-f*d)
=m1.g.h.sin (alpha)-f*d
or h=d ==>
Ec (m1)= (m1.g.sin (alpha)-f)*d
Non?
Pourquoi la somme des deux masses m1+ m2 dans l'énergie cinétique finale?:
... parce que les 2 masses sont en mouvement et animées de la même vitesse v.
On a donc :
Energie cinétique de la masse 1 : Ec1 = 1/2 . m1 * v²
Energie cinétique de la masse 2 : Ec2 = 1/2 . m2 * v²
Et donc l'énergie cinétique de l'ensemble des 2 masses est : Ec = Ec1 + Ec2
Ec = 1/2 . m1 * v² + 1/2 . m2 * v²
Ec = 1/2 . (m1+m2) * v²

Pour la partie 2, lire évidemment : Soit d la distance que m1 continuera à avancer sur le plan incliné, on a: ...
Pour la partie 2, pendant que la masse m1 continue à monter :
La norme de la composante du poids suivant la direction du plan incliné est m1.g.sin(alpha) et elle est dirigée vers le bas du plan
Le mouvement est vers le haut du plan, la force de frottement f s'oppose au mouvement et donc la force de frottement est dirigée aussi vers le bas du plan.
La résultante de ces 2 forces a pour norme (mg.sin(alpha) + f) et elle est dirigée vers le bas du plan.
Le travail de cette résultante de force sur le parcours de distance d (force et trajet de même direction mais de sens contraire) est W = - (mg.sin(alpha) + f) * d
Et c'est ce travail qui va "manger" l'énergie cinétique de la masse 1 jusqu'à l'arrêt --> Ec + W = 0
1/2 . m1 * v² - (m1.g.sin(alpha) + f) * d = 0
(m1.g.sin(alpha) + f) * d = (1/2).m1*v²
(1 * 10 * 1/2 + 2) * d = (1/2)*1*1,55²
d = 0,17 m
Sauf distraction. 
Ok
j'ai compris maintenant presque tout
sauf égalité de P= mg.sin (alpha)
D'où vient ce sin (alpha ) là ?
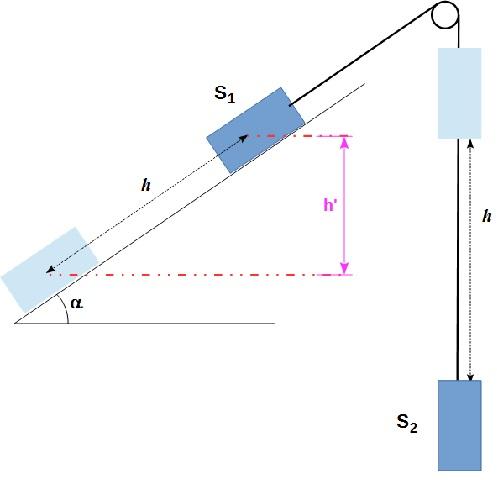
beugg ce qui vous pose problème, me semble-t-il, c'est que vous n'avez pas compris que lorsque le solide S2 descend d'une hauteur h, il n'en est pas de même du solide S1.
S1 glisse bien sur le plan incliné d'une hauteur h, mais son centre d'inertie ne s'élève QUE d'une hauteur h' = h sin  (cf figure).
(cf figure).
Le travail moteur du poids de S2 est : W2 = m g h mais le travail résistant du poids de S1 est : W1 = - m g h'
c'est à dire encore : W1 = - m g h sin 
***Image recadrée***


