je vois pas comment on peut exprimer h pas en fontion de .

b) Calculer la valeur de la vitesse de la bille lorsque l'angle que fait le fil avec la verticale a pour valeur

Salut!
W(P)=mgl*(1-cos0)
Mais c'est dur à expliquer sans schéma.

Je ne sais pas de quel h tu parles.
On te demande de calculer le travail du poids.
Tu dois avoir une formule dans ton cours.
De mémoire, avec des notations qui ne sont probablement pas les tiennes :

où est le vecteur correspondant à un déplacement infinitésimal, ici :
- de norme ,
- faisant un angle avec l'horizontale ou la verticale (à regarder).

Il ne reste plus qu'à exprimer le produit scalaire, et à intégrer.

A nouveau, désolé pour les notations.

Salut Nicolas
En 1ère on ne voit pas encore les intégrales

euh en niveau première par je connais pas encore les intégrales

et la_fuereur pk et pas ?

Tu as raison, elda, c'est .
Et désolé pour les intégrales : c'est l'enthousiasme !

en fait j'avais un doute car il y a la réponse à peu près effacer sur la feuille qu'on m'a passer mais ça pas l'air d'être exprimer en fonction de et , mais ça doit juste être parce que c'est pas lisible, merci beaucoup à tous les 2!!!!!

cos = cos 0 = 1 non?

non alpha est un angle entre 0 et 40°

Ok j'avais mal compris désolé

la_fureur, l'énoncé demande à calculer le travail entre l'angle =40° et l'angle quelconque.

En y réfléchissant, c'est pas plutôt
W(P)=mgl*(1-cos(0-))

car W(P)=mgh
avec h= l-l*cos(0-)
=l*(1-cos(0-))
non?

la_fureur, je ne crois pas.

ok

a)
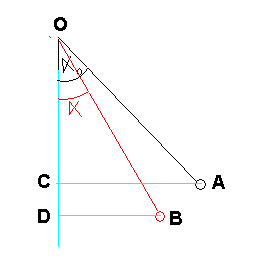
OC = OA cos(alpha_o)
OD = OB.cos(alpha)

CD = OD - OC et avec OA = OB  = L, il vient:

CD = L.(cos(alpha) - cos(alpha_0))

Le travail du poids entre les angles alpha_0 est alpha = m.g.CD.

Le travail du poids entre les angles alpha_0 est alpha = m.g.L.(cos(alpha) - cos(alpha_0))
-----
b)
Le travail du poids se transforme en énergie cinétique.
Pour l'angle alpha, on a donc:

(1/2).m.v² = m.g.L.(cos(alpha) - cos(alpha_0))
avec v la vitesse de la billle pour l'angle alpha.

v² = 2.g.L.(cos(alpha) - cos(alpha_0))

...
-----
Sauf distraction.  

merci J-P, justement j'allais demander une vérification donc pour le début c'est bon merci beaucoup.

Caculer sa vitesse en B:

j'ai fait:






c)Le pendule oscille autour de sa position d'équilibre. Pour quelles valeurs de la vitesse de la bille est-elle nulle?

comme on a négligé les frottements et que la force exercée par le fil n'entre pas en jeu, ça sera toujours (on peut le retrouver par le calcul)
en fait c'est le moment où elle va repartir dans le sens contraire.

d) On recommence l'expérience en plaçant une butée en C. Le point C est sur la verticale passant par O, à 12 cm en dessous de O.

A quelle hauteur remonte la bille? Conclure

j'ai fait:





  (au passage =68.69°)



mais là je suis pas sûre du tout, et il faut conclure quoi?

une petite réponse ? au moins sur le début?

la d) est fausse je viens de le voir. un peu d'aide svp

j'ai 17.8, mais ne vous embêtez, c'est plus la peine, c'était pas pour moi et la personne aura la reponse demain.
merci quand même

c)
OK pour alpha_o mais il y a aussi -alpha_o, c'est à dire aux 2 extrémités de la trajectoire de la bille.

d)
Tu devrais trouver que la bille remonte à la même altitude que le point O.

Sauf distraction.  

on m'a dit que pour la d) c''était la même hauteur que le point A, mais je vois pas comment. Est ce que quelqu'un peut m'expliquer car moi j'ai trouvé h=2l(1-cos alpha0)

merci beaucoup

Oui, c'est ce que j'ai voulu écrire.

La bille remonte à la même altitude que le point A.

La raison:
L'énergie mécanique du système reste constante.

en alpha_o, l'énergie potentielle de la bille est mg.CD et l'énergie cinétique de la bille est nulle.

Energie mécanique = Energie potentielle + énergie cinétique.
Et donc:
Energie mécanique = mg.CD + 0

Energie mécanique = mg.CD
-----
L'énergie mécanique reste la même,même avec une butée en C.
Le fil s'appuie en C et la bille remonte de l'autre coté jusqu'au moment où elle s'arrète (et va repartir dans l'autre sens), elle est alors au point le plus haut qu'elle peut atteindre.
Comme la bille a, à cet instant, une vitesse nulle, son énergie cinétique est nulle et donc toute l'énergie mécanique est en fait de l'énergie potentielle.

Avec h l'altitude (par rapport au point D de mon dessin) de la bille à cet instant:

On a donc mgh = mg.CD

--> h = CD

Soit la même altitude que le point A de mon dessin.
-----
Sauf nouvelle distraction.  

thanks a lot!

Forget it.

salut à tous !!! j'ai cet exo à faire pour la rentrée, et, ne comprenant pas, je suis venu sur votre site. Cependant dans le 1°, je ne comprend la formule CD = L.(cos(alpha) - cos(alpha_0)). Merci de m'aider...

Aidez-Moi plz :'(:'(