Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

Énergie cinétique.

Posté par
kamikaz 13-02-20 à 21:39

Bonsoir,

Le poids total d'une voiture en charge est P=13000N .
Le conducteur démarre , abordé une côte avec une vitesse de 10km/h puis atteint son sommet avec une vitesse V=40km/h . La distance parcourue sur ce trajet est de 500m  et la ligne de plus grande pente est de 15°.
Du sommet de la côte , la voiture aborde une partie horizontale de la route en maintenant sa vitesse constante sur une certaine distance , avant de freiner sur une distance de 10m .

1-1) déterminer la force motrice de la voiture durant son trajet sur la côte .

1-2) sur le plan horizontal pendant que sa vitesse est constante.

2) déterminer la force de freinage de la voiture.

Posté par
odbugt1re : Énergie cinétique. 13-02-20 à 23:36

Bonsoir,

Peut être pourrais tu exposer ou tu en es de tes recherches .....

Posté par
kamikazre : Énergie cinétique. 14-02-20 à 07:54

Bonjour
1-1) Système : la voiture
Référentiel : référentiel terrestre supposé galliléen
Bilan des forces : force motrice F , force de frottement f, le poids P et la réaction R .
Application du théorème de l'énergie cinétique.

∆Ec=W AB(Fext)

EcB-EcA=WABf +WABF +WABP+WABRn

\dfrac{1}{2} mVA²-\dfrac{1}{2} mVB²=f×AB +Psin×AB car Rn AB .

\dfrac{1}{2} mVA²-\dfrac{1}{2} mVB²=AB(f+Psin+F)

F=\dfrac{m(VB²-VA²)}{2×AB}+mg(sin+0,6)

Application numérique :

F=\dfrac{1300(11,11²-2,77²}{2×500}+13000(sin15°+0,6)=11315,13N.

Posté par
odbugt1re : Énergie cinétique. 14-02-20 à 09:44

La démarche que tu utilises est correcte, mais certains points sont à revoir :

a) L'énoncé ( c'est regrettable) reste muet au sujet des forces de frottements. Tu n'as donc aucun moyen de calculer le travail de ces forces et tu seras obligé de les considérer comme étant négligeables.

b) Le calcul du travail du poids est à revoir : Il n'est pas égal à P*sin(α )

Posté par
kamikazre : Énergie cinétique. 14-02-20 à 13:43

Oui , les forces de frottement f =0,6×P

Il n'est pas égal à P*sin(α ) mais à quoi ?

Posté par
odbugt1re : Énergie cinétique. 14-02-20 à 14:14

Citation :

Oui , les forces de frottement f =0,6×P
J'ignore d'où tu sors cela. l'énoncé n'en parle pas.

Il n'est pas égal à P*sin(α ) mais à quoi ?
J'ai voulu dire (et je confirme) :
Il n'est pas égal à P * sin(α ) * AB


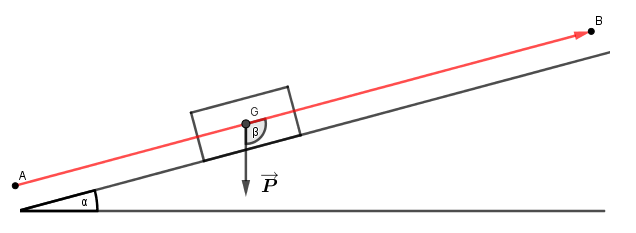
Le travail d'une force constante d'intensité F sur un déplacement rectiligne AB est égal à
W = F * AB * cos (angle entre les vecteurs \vec F et \vec {AB})
Voir schéma ci-dessous.

Énergie cinétique.

Posté par
kamikazre : Énergie cinétique. 14-02-20 à 14:25

L'énoncé indique f=P×0,6

Posté par
odbugt1re : Énergie cinétique. 14-02-20 à 14:35

Donc W(\vec P) = P * AB * cos()
Or  cos() = - sin ()
W(\vec P) = - P * AB * sin ()

Posté par
gts2re : Énergie cinétique. 14-02-20 à 19:34

Bonjour,

Juste une remarque sur le 0,6 : c'est une valeur élevée : pour une voiture classique, on a un coefficient de 0,015. Personne n'arriverait à pousser une voiture avec un tel coefficient.

Posté par
kamikazre : Énergie cinétique. 16-02-20 à 07:48

Bonjour gts2 , l'énoncé donne f=0,6 P

Posté par
kamikazre : Énergie cinétique. 16-02-20 à 08:17

odbugt1

cinétique.

∆Ec=W AB(Fext)

EcB-EcA=WABf +WABF +WABP+WABRn

\dfrac{1}{2} mVB²-\dfrac{1}{2} mVA²=f×AB -Psin×AB car Rn AB . \\ \\ \dfrac{1}{2} mVB²-\dfrac{1}{2} mVA²=AB(f-Psin+F) \\ \\ F=\dfrac{m(VB²-VA²)}{2×AB}+mg(sin-0,6)

Application numérique :

F=\dfrac{1300(11,11²-2,77²}{2×500}+13000(sin15°-0,6)=-4284,86N
F=4284N .

2) sur le plan horizontal , pendant que sa vitesse est constante on a :

∆EC=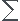 W BCF(ext)=
Or ECC =ECB , WBCP =0 J , WBCR =0J.

Donc WBCf+WBCF=0

F×d=f×d
F=f

F=7800N.

3) la force de freinage ,

Soit f' la force de freinage .

Si on considère que la voiture freine au point C , alors ECC=0

D'où ECC-ECB=WBCF +WBCf +WBCf' or WBCF=0

Donc ECC-ECB
=-f×d+f×d

ECB=f×d+f'×d

f'=\dfrac{mVB²}{2d}

f'=223N

Posté par
gts2re : Énergie cinétique. 16-02-20 à 08:29

Bonjour,

Il n'y aurait pas un problème de signe ? : sin(15)+0,6, ce qui permettrait d'avoir une force F>0.

Posté par
kamikazre : Énergie cinétique. 16-02-20 à 09:07

Bonjour , non !

Posté par
kamikazre : Énergie cinétique. 16-02-20 à 09:07

Voyez vous même !

Posté par
odbugt1re : Énergie cinétique. 16-02-20 à 09:42

Il y a bien un problème de signe !
Le résultat numérique correct est bien celui trouvé par kamikaz dans son post du 14-02-20

J'ai cru repérer une erreur de signe sur le travail du poids, mais en réalité je n'ai pas fait attention que kamikaz avait aussi changé les signes de la variation de l'énergie cinétique.
De plus je ne comprenais pas à cette date du 14-02-20)  l'origine du " 0,6 "

Posté par
odbugt1re : Énergie cinétique. 16-02-20 à 10:20

\Delta E_c = W( \overrightarrow{F} ) + W( \overrightarrow{f} )+W( \overrightarrow{P} ) \\ \\ \Delta E_c = 0,5*1300*(11,1^2-2,77^2)=7,52.10^4~J \\ \\ W( \overrightarrow{f} )= - 0,6 * 13000 * 500 = -3,90.10^6~J \\ \\ W( \overrightarrow{P} )= - 13000 * 500 * sin(15°)= -1,68.10^6~J \\ \\ W( \overrightarrow{F} )= 7,52.10^4 + 3,90.10^6 + 1,68.10^6 = 5,66.10^6~J \\ \\ F= \dfrac{5,66.10^6}{500} =11310~N \\

Posté par
kamikazre : Énergie cinétique. 16-02-20 à 11:43

Oui on retombe sur mon résultat du départ .

Posté par
Amerkel868re : Énergie cinétique. 20-11-22 à 21:44

Excuse moi kamikaz comment tu as fait pour trouver la force de freinage puis que  tu n'as pas fais l'application numérique et tu trouves 223N j'aimerais que tu m'explique

Posté par
odbugt1re : Énergie cinétique. 21-11-22 à 08:42

Bonjour,

Kamikaz a écrit      f'=\dfrac{mV_B²}{2d}
alors que la relation correcte est :

f'=\dfrac{mV_B²}{2d} - f

C'est un simple oubli car avec la relation correcte on obtient bien f' = 223N

f'= \dfrac{1300*11.11^2}{2*10} - (0,6*13000) = 223N


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !