Inscription / Connexion Nouveau Sujet
energie cinetique
Bonjour
SVT pouviez-vous m'aider sur cet exercice?
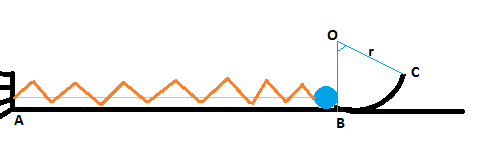
un jouet est constitué d'une gouttière ABC (voir figure ci-contre).
AB est horizontal, BC est un arc de cercle de centre O et de rayon r=50cm. O et B se trouve sur la même plan verticale. La gouttière se trouve dans un plan vertical.
Une masse m=100g peut être mise en mouvement grace à un ressort, de raideur k=10N/m, que l'on comprime à l'aide d'une tirette T. Les frottements sont néglisables sur tout le long de la gouttière.
1) Trouver la compression qu'il faut imprimer au ressort pour qu'il puisse envoyer la masse m jusqu'en C avec vitesse nulle. On donne =60°.
2) On imprime maintenant au ressort une dimunition de x=0,4m.
a) Trouver la vitesse de la masse m au passage par le point C.
b) Déterminer la vitesse de la masse m lorsqu'elle tombe au sol.
Je propose :en utilisant la variation de Ec on a:
1) ∆Ec= W(P)+W(R)+W(T)→Ecc-Eca=mgh-1/2kx² or h=r(1-cosα) et en C Vc=0
→Ec=mgr(1-cosα)-1/2kx²→1/2mv²=mgr(1-cosα)-1/2kx²
1/2(mv²+kx²)=mgr(1-cosα)→x=√ [m(v²+2gr(1-cosα)/k]
Dans l'enonce on m'a pas donné la vitesse v jarrive pas a calculé la valeur de x donc j'ai besoin d'aide pour savoir comment faire
Bien que ce ne soit pas dit clairement dans l'énoncé on fait l'hypothèse que la masse n'est pas solidaire du ressort.
Avant le départ de la masse le ressort possède une énergie potentielle élastique telle que :
Epe = (1/2) * k * ( x)²
x)²
Au moment précis " t " où la masse cesse d'être en contact avec le ressort on fait l'hypothèse que la totalité de l'énergie potentielle du ressort a été transférée à la masse sous forme d'énergie cinétique.
L'énergie cinétique initiale de la bille ( à l'instant " t " ) est donc égale à (1/2) * k * ( x)²
x)²
On se sert ensuite de la conservation de l'énergie mécanique entre l'instant "t" et l'arrivée de la masse en C et on obtient ainsi une relation qui permet d'exprimer et de calculer la compression ( x) qu'il a fallu donner au ressort.
x) qu'il a fallu donner au ressort.
Bonjour Odbugt
On n'a pas vu la leçon sur l'energie potentille.Je propose qu'on utilise la variation de Ec
Si je comprends bien votre explication je propose :
Système{bille +ressort}
Le ressort comprimé possede : W(T)=1/2.k.X² et cette energie est transférée sous forme d'energie cinetique au moment ou la masse quitte le ressort.Donc on a : W(T)=1/2.k.X²=Eci=1/2mv²i
En utilisant la variation de Ec : ∆Ec= W(P) ,Ecf-Eci=-mgh or Ecf =0 car Vc =0 donc Eci=mgh avec h=r(1-cosα) or Eci=1/2.k.X² donc on a : 1/2.k.X²=mgr(1- cosα) entraine : X=√[2 mgr(1- cosα)/k].
AN :X=√[2x0.1x9.8x0.5x(1-cos60°)/10]=0.22m
2) ∆Ec= W(P) ,Ecf-Eci=-mgh =- mgr(1- cosα)
1/2mv²c-1/2.k.X²=-mgr(1- cosα) entraine v²c=[k.X²-2mgr(1- cosα)]/m
Vc=√[k.X²-2mgr(1- cosα)]/m
AN : Vc=√[10x0.4²-2x0.1x9.8x0.5x(1-cos60°)]/0.1= 5.71m/s
Question 1 :
OK
Question 2 :
OK pour l'analyse et pour le résultat littéral.
Toutefois, je ne trouve pas le même résultat numérique que toi.
bonjour
ok j'ai refait mon calcul je trouve Vc= 11.1 m/s
pour la question 3) je propose ceci:
∆Ec= W(P) ,Ecf-Eci=mgh avec h=r(1-cosα) et Ecf=1/2mV²s ,Eci=1/2mV²c
1/2mV²s -1/2mV²c=mgr(1-cosα) →V²s=V²c+2gr(1-cosα)
Vs=√[11.1²-2x9.8x0.5x(1-cos60°)]=10.87m/s
Question2 :
J'ai trouvé VC = 3,33 m/s
Question 3 :
Ici encore, je suis d'accord avec ton expression littérale mais pas avec ton calcul numérique
On peut aussi dire :
Entre le moment où la masse quitte le contact du ressort et le moment où elle reprend contact avec le sol en S le travail du poids est nul.
Donc la masse conserve en S son énergie cinétique initiale :
(1/2) * k * ( x)² = (1/2) * m * (VS)²
x)² = (1/2) * m * (VS)²


