Inscription / Connexion Nouveau Sujet
Energie cinétique
EXERCICE:
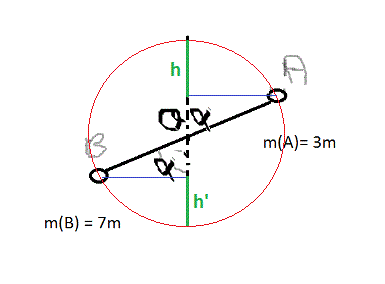
un pendule est constitué d'une tige deAB = 2L et M=6m tel que m =50g ET L=0.8m
cette tige est munie de deux masselottes quasi ponctuelles en A et B elles ont pour masse
m(A) = 3m et m(B) =7m
le pendule composé oscille sans frottement
1/ calculer le moment d'inertie J du pendule pesant ainsi constitué
2/ on écarte le pendule d'un angle alpha ( voir figure) (alpha) = 50°[/rouge]. on le lache sans vitesse initiale.
calculer la vitesse angulaire w0 lorsque celui ci passe par sa position verticale.
3/ calculer alors la vitesse VB de la masselote placée en B
 merci d'avance
merci d'avance
1) il suffit d'appliquer aux deux masses la formule qui donne le moment d'inertie d'une masse ponctuelle I = mR² (donc J = 7mL² + 3mL² = 10mL² = ...
2) utilise la conservation de l'énergie totale (cinétique + potentielle) entre le moment initial et la position verticale.
3) VB = L . w0
SVP j arrive a pas a comprendre la deuxieme question je veux utiliser le theoreme d energie cinetique les forces appliquees seront le poids ou quoi aidez moi svp
Quelle est la différence d'altitude h entre le point où la masse A se trouve au départ et lorsqu'elle est à la verticale au dessus du point de pivot O ? (en fonction de L et de alpha) ?
Le travail du poids de la masse A entre ces 2 positions, pourra se calculer par - m(A) * g * |h|
Pareillement pour la masse B :
Quelle est la différence d'altitude h' entre le point où la masse B se trouve au départ et lorsqu'elle est à la verticale en dessous du point de pivot O ? (en fonction de L et de alpha) ?
Le travail du poids de la masse B entre ces 2 positions, pourra se calculer par + m(B) * g * |h'|
L'énergie cinétique du pendule passant par la verticale est alors la somme changée de signe du travail du poids de A et du travail du poids de B
Et on a aussi Ec = 1/2.J.W² ... qui permettra de calculer W au passage par la verticale du pendule.
Essaie ...
la difference de hauteur dans les deux cas est L.sin alpha.
Alors la variation de l energie cinetique est egale a la L.g.sin alpha(mA+mB). et on obtient W0. nLa derniere question demande la vitesse de la maselotte en B est ce que c la meme vitesse de la tige jsp comment faire
la difference de hauteur dans les deux cas est L.sin alpha.
Alors la variation de l energie cinetique est egale a la L.g.sin alpha(mA+mB). et on obtient W0. nLa derniere question demande la vitesse de la maselotte en B est ce que c la meme vitesse de la tige jsp comment faire
"la difference de hauteur dans les deux cas est L.sin alpha. "
Ce n'est pas correct.
Et même cela corrigé, il reste d'autres des erreurs.
La masse A monte ... et donc le travail de son poids est négatif.
La masse B descend ... et donc le travail de son poids est positif.
Et donc ...
Bonjour,
Ecris sur le site tout ce que tu as fait pour les 2 premières questions... En suivant ce qui a été écrit dans le message 25-10-25 à 16:43
Si c'est correct, on verra pour la suite.
Voice ce que j ai fait pour les deux premiere questions.
Excusez moi j'arrive pas a ecrire cela avec le clavier.
Je commence par ne pas avoir la même réponse à la question 1 ...
1)
J = (1/12).M*(2L)² + M(A)*L² + M(B)*L² = 2m.L² + 7m*L² = 12.mL² (= 12 * 50.10^-3 * 0,8² = 0,384 kgm²)
2)
h = L*(1-cos(alpha))
W(PA) = - M(A) * g * h = - 3mgL(1-cos(alpha))
h' = L*(1-cos(alpha))
W(PB) = M(B) * g * h' = 7mgL(1-cos(alpha))
W(Poids) = W(PA) + W(PB) = 4mgL(1-cos(alpha))
E(cin) = 4mgL(1-cos(alpha)) = 4 * 50.10^-3 * 9,81 * 0,8 * (1 - cos(50°))
E(cin) = 1/2 * J * w²
4mgL(1-cos(alpha)) = 1/2 * J * wo²
4mgL(1-cos(alpha)) = 1/2 * 12mL² * wo²
4g(1-cos(alpha)) = 6.L * wo²
wo² = 2/3 * g/L * (1-cos(alpha)) = 2/3 *9,81/0,8 * (1-cos(50°)) = 2,92
wo = 1,71rad/s
vo = wo * L = 1,71 * 0,8 = 1,37 m/s
***************
Il te reste à voir si c'est correct ou non ...
Et si oui, chercher tes erreurs.
En préalable ...
Voir si on doit ou non limiter le nombre de chiffres significatifs des réponses déjà faites en respectant les "règles".
-----
La question 3 est, je pense la vitesse quand la masse B passe par le point bas, donc tige verticale.
Comme on a trouvé la vitesse angulaire à cet instant (wo = 1,71 rad/s)
La vitesse de la masse B à cet instant est v(B) = Wo*L = 1,37 m/s
(je l'ai noté; par distraction, vo dans ma réponse précédente)
****
Si maintenant ce qui est demandé (ce n'est pas clair) est la vitesse de la masse B en fonction du temps, ce n'est pas bien difficile, mais on aboutira à une équation différentielle que l'on ne peut pas résoudre avec des fonctions élémentaires
C = (7m-3m)*g*L.sin(alpha) = J.d²alpha/dt²
4m*g*L.sin(alpha) = 12.mL².d²alpha/dt²
d²alpha/dt² = 1/3 * g/L.sin(alpha)
d²alpha/dt² = 1/3 * 9,81/0,8.sin(alpha)
d²alpha/dt² = 4,1 .sin(alpha)
Et là on ne peut pas trouver alpha en fonction du temps ... sauf par exemple en utilisant des fonctions spéciales de Jabobi .. qui ne sont pas au programme (du moins cela m'étonnerait très fort)
Si on le fait quand même, alors on tire l'expression de w en fonction du temps en intégrant et puis v en multipliant par L
Mais je ne pense pas que c'est cela que l'auteur veut (même si la question est sujette à interprétation).
Ok mais dans la question 2 le moment d'inertie qu'on a utilise c celui total de la question 1 n est ce pas
Ok mais dans la question 2 le moment d'inertie qu'on a utilise c celui total de la question 1 n est ce pas
Bien évidemment.
Attention que dans le message du 19-12-16 à 10:33, il y avait une erreur pour la réponse à la question 1, le moment d'inertie de la tige du pendule avait été oublié dans cette réponse.