Inscription / Connexion Nouveau Sujet
encore un pendule mais sa vitesse reste constante ?
Bonjour voici un énoncé qui me laisse perplexe !
Un pendule de masse 100g est accroché au bout d'un fil de masse négligeable
La ditance est de 25 cm entre le cdg du pendule et l'endroit ou il est fixé.
Calculer la vitesse linéaire de rotation du pendule pour que l'angle constant pris par le fil soit de 15° par rapport a la verticale.
Au début j'ai foncé dans un énième exo sur la vitesse du pendule lorsqu'il passe a la verticale ; mais je remarque que l'on veut une "vitesse linéaire de rotation" cela doit etre Vt ?
Il y a la force d'inertie a trouvé je pense ou l'accélération normal (an = V2 / r)...ce que je sais c'est plus ca va aller vite + l'angle sera grand .
Je ne sais pas du tout comment débuter ce probleme !
j'ai peut etre un truc :
comme P = 1 N alors les force d'inetrie T = P sin 15
par la suite accelération an =2.588 m.s-2
D'ou Vt = 0.129 m.s-1 (car le rayon vaut r = 0.25 x cos 75 = 0.0647 m)
Bon ben j'ai enfin trouver tout seul
m . An
il suffisait de dire que Tan 
= ---------
m . g
V carre
avec An = --------- on obtient : V = 
g.r.Tan
r
V = 0,8 m.s
merci a moi tout seul 
apparement je me serai enflammé tout seul :
je trouve finalement w = 3,21 rad.s et v = 0,208 m.s
Quelqu'un pourrait confirmer quelques choses
Merci
J'ajoute un petit shema ca fera peu etre venir les gens ...
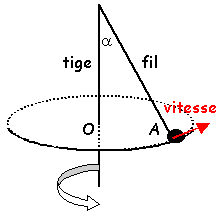
Bonjour,
Je suis d'accord avec l'expression littérale trouvée :
et puisque, en notant L la longueur du fil, r = L.sin()
Mais je ne comprends aucune de tes applications numériques. Peux-tu vérifier ?
en fait j'ai oublié de prendre la vrai valeur du rayon (L.sin)
Ma dernière réponse est celle que tu m'as simplifié moi j'arrivais à :
V = L.sin x ( g / (L.cos)= 0.41m.s-1
car je suis passé par W qui vaut: W = (g / L.cos) = 6.43 rad.s-1
Ca y est cette fois je crois que tout est dis merci de ton aide "coll"
: en utilisant le bouton 
qui est en bas du cadre d'écriture (entre "POSTER" et "Aperçu")
Annuler
connectez vous