Inscription / Connexion Nouveau Sujet
En Physique : angle de déviation
Le but ce cette exercice est d'étudier l'angle de déviation d'un rayon lumineux qui se réfléchit sur un miroir d'angle.
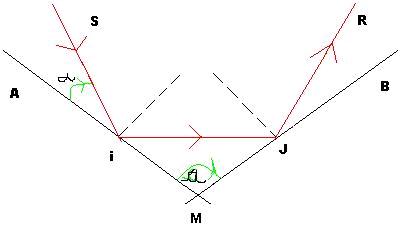
La figure ci-dessous représente la coupe AMB de miroir dans le plan d'incidence .L'angle entre les deux plans du miroir est (MA ;MB)= a l'angle du rayon incident est (IA;IS) = alpha
La figure:ci dessous a la fin
Et les Quéstion :
Pardonnez pour les vecteurs mes je n'arrive pas à les montrés enfin je n'arrive pas a mettre la fleche représentative au dessus de.
1)ON me demande de calculer les angles en fonctions de alpha et de a.
a)(IS;IJ) b)(JM;JI) c) (JI;JR)
Je ny arrive pas pour cette quéstion et je ne comprends pas donc ces super !
2)on me demande ensuite d'en déduire une valeur de langle de dérivation (SI;JR) et dans constater quelques choses.
Sans la première question cela me parait difficile...
3)Puis la derniere quéstion me demande en quel valeur (a) permet au rayon incident et réfléchi sont-ils parralléles? et perpendiculaires?
Je n'ai réussi a repondre qu'au premier angle :
1)pour l'angle (IS;IJ)
tu as IA;IS)=
or d'aprés les lois de la réfraction
tu as : (IA;IS)=(IJ;IM)=
donc : (IS;IJ)=180°-2(IA;IS)=180°-2
Je pense ne pas me tromper, pouvez vous m'aider pour les autres questions, merci.
ERREUR :
Le but ce cette exercice est d'étudier l'angle de déviation d'un rayon lumineux qui se réfléchit sur un miroir d'angle.
La figure ci-dessous représente la coupe AMB de miroir dans le plan d'incidence .L'angle entre les deux plans du miroir est (MA ;MB)= a l'angle du rayon incident est (IA;IS) = ALPHA
La figure:ci dessous a la fin
Et les Quéstion :
Pardonnez pour les vecteurs mes je n'arrive pas à les montrés enfin je n'arrive pas a mettre la fleche représentative au dessus de.
1)ON me demande de calculer les angles en fonctions de ALPHA et de a.
a)(IS;IJ) b)(JM;JI) c) (JI;JR)
Je ny arrive pas pour cette quéstion et je ne comprends pas donc ces super !
2)on me demande ensuite d'en déduire une valeur de langle de dérivation (SI;JR) et dans constater quelques choses.
Sans la première question cela me parait difficile...
3)Puis la derniere quéstion me demande en quel valeur (a) permet au rayon incident et réfléchi sont-ils parralléles? et perpendiculaires?
Je n'ai réussi a repondre qu'au premier angle :
1)pour l'angle (IS;IJ)
tu as IA;IS)=ALPHA
or d'aprés les lois de la réfraction
tu as : (IA;IS)=(IJ;IM)=ALPHA
donc : (IS;IJ)=180°-2(IA;IS)=180°-2ALPHA
Je pense ne pas me tromper, pouvez vous m'aider pour les autres questions, merci.
Bonjour,
Relation de Chasles encore et toujours !
(JM ; JI) = (BM ; MA) + (IA ; IS) + (IS ; IJ) + (IJ ; JI)
En utilisant ce que tu as déjà démontré, à savoir que (IS ; IJ) =  - 2
- 2

Donc (JM ; JI) = (BM ; MA) + (IA ; IS) + (IS ; IJ) + (IJ ; JI)
= 180 + a + ALPHA + 180 - 2ALPHA + 180
= 3pi + a + ALPHA
C'est ça ?

Il faut être très rigoureux pour ce type d'exercice.
Tout d'abord  - 2
- 2 n'est pas égal à
n'est pas égal à 
Mais, s'il est vrai que (BM ; MA) =  + (MB ; MA)
+ (MB ; MA)
il est faux que (MB ; MA) = a
C'est (MA ; MB) qui est égal à a

Je suis un peu mal à l'aise avec ce qui a été fait.
Avec les conventions habituelles, le alpha indiqué sur le dessin est négatif.
Exemple numérique:
Avec (IS;IJ) = 180° - 2ALPHA
Si par exemple alpha = -30°, on trouverait (IS;IJ) = 180 - 2*(-30°) = 240°
Mais pour moi, on aurait du avoir (IS;IJ) = -240° ou bien (IS;IJ) = 120°
-----
Mais tout n'est que question de conventions ...

Donc (JM ; JI) = (BM ; MA) + (IA ; IS) + (IS ; IJ) + (IJ ; JI)
= -PI - a + ALPHA + PI - 2PI + PI
= PI - a - ALPHA
Comme ça ?
Bonjour J-P  (oui, que a et
(oui, que a et  soient deux valeurs négatives ne met pas à l'aise, cela complique inutilement l'exercice).
soient deux valeurs négatives ne met pas à l'aise, cela complique inutilement l'exercice).
Oui Geoffrey92 : je suis d'accord avec (JM ; JI ) =  - a -
- a - 
Continue, tu es presqu'au bout...

Et si je fais :
on a : (IJ;IM)+(MI;MJ)+(JM;JI)=180°
donc : (JM;JI)=180°-ALPHA-a
Est ce que l'on peut utiliser la relation de Chasles comme ça ?
Voir mes messages de 11 h 55 et 12 h 37
(BM ; MA) = (BM ; MB) + (MB ; MA) =  + (MB ; MA)
+ (MB ; MA)
Donc il est faux d'écrire que (BM ; MA) = - - a
- a

Oui Coll,
alpha négatif, soit ...
Mais alors le résultat trouvé soit (IS;IJ) = 180° - 2ALPHA
n'est pas correct...
Il y a une erreur de signe.
Si je ne me trompe.

Je confirme bien (IS ; IJ) =  - 2
- 2 
(IS ; IJ) est supérieur à un angle plat, supérieur à  et avec
et avec  < 0 c'est bien cela...
< 0 c'est bien cela...
D'autre part (mécaniquement) (IS ; IJ) = (IS ; IA) + (IA ; IM) + (IM ; IJ) = - +
+  -
-  =
=  - 2
- 2

Ah oui, distraction.
Mon exemple numérique donne bien (IS;IJ) = 180 - 2*(-30°) = 240°
Et c'est juste.

Pour l'angle (JI,JR) je pense à ça ... :
(JM,JI)+(JI,JR)+(JR,JB)=
D'après loi de reflexion : (JM,JI)=(JR,JB)= -a-
-a-
donc (JI,JR)= -2(
-2( -a-
-a- )
)
=2a+2 -
-
=2(a+ -(
-( /2))
/2))
Tu penses bien 
Il reste à ajouter tout cela (tu as fait le plus pénible) et tu pourras ainsi "en constater quelque chose"

J'en suis à la dernière question.
Les rayons incidents et réfléchi sont bien parallère si a=180° et perpendiculaire si a=90° ? Si la reflexion est possible bien sure ...


