Bonjour,
Comme il s'agit d'un carré,  la résultante des deux forces issues des charges q est colinéaires à la force issue de Q.
Tu vois déjà que q et Q seront de signe opposé.
Un petit calcul de geometrie va te mener au résultat.

C'est très bien jusque là ...

Il manque juste ce qu'il faut pour indiquer les directions et sens des forces... pour pouvoir faire la somme vectorielle.

FQ/Q et la résultante des 2 forces exercées par les q sur Q sont sur une même diagonale du carré (à justifier)

Il faut donc que : K.Q²/2a² + K.q.Q /a² * V2 = 0

Q/2 + q * V2 = 0

q = - Q/(2V2)

Sauf distraction.  

Merci sanantonio312 et J-P.

J-P: merci tout particulièrement pour cette correction très claire.

Cordialement

bonjour,
J-P, je ne comprends pas quelque chose: si K.Q²/2a² + K.q.Q /a² * V2 = 0 donc une des deux forces est négative et je vois pas comment une force peut etre négative, je pensais qu'il fallait que K.Q²/2a² = K.q.Q /a² * V2 et du coup je me retrouvais avec Q = q * 2V2
merci de votre aide

Autre approche (plus longue) mais peut-être plus parlante.



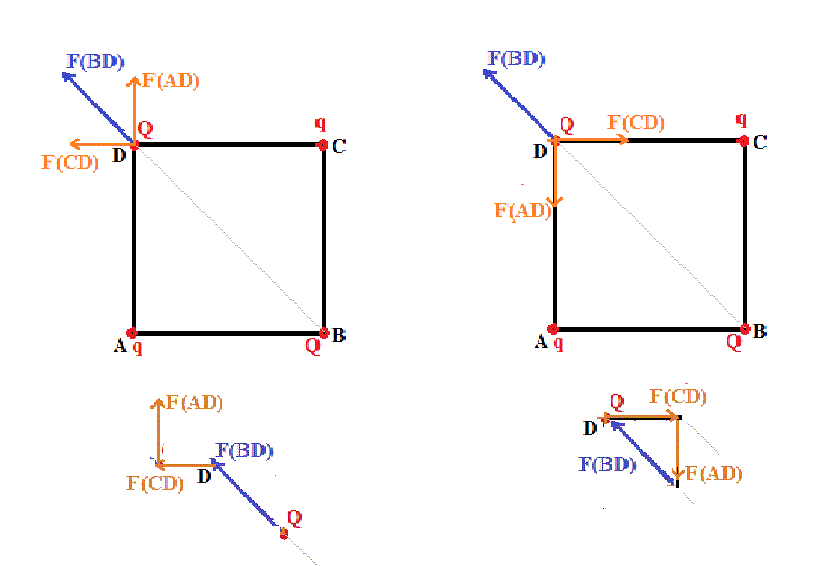
Si les charges Q et q sont de même signe et non nulles ... on est dans le cas du dessin de gauche.

Il est impossible que la somme vectorielle des forces sur la charge Q (par exemple celle en D) provenant des 3 autres charges soit nulle.
Et donc Q et q doivent forcément être de signe contraire.
-----
Si les charges Q et q sont de signes contraires ... on est dans le cas du dessin de droite.

Il est possible alors que la somme vectorielle des forces sur la charge Q (par exemple celle en D) provenant des 3 autres charges soit nulle.

Il suffit pour cela que |F(AD)|² + |F(CD)|² = |F(BD)|²

et comme |F(AD)| = |FCD| --->  |F(BD)| = V2 * |F(AD)|

k.|Q*Q|/(V2.a)² = V2 * k.|Q*q|/a²

|Q|/2 = V2 * |q|

|Q| = 2V2 * |q|

Et on sait que Q et q sont de signes contraires ---> Q = - 2V2 * q

q = - Q/(2V2)