Inscription / Connexion Nouveau Sujet
Éléctrocinetique besoin simple exercice application de formule
Bonjour, j'ai besoin d aide pour reussir ce type d'exercice simple, je ne sais pas du tout par quoi commencer ou par quoi chercher a part faire la somme des resistances en parallèles (les resistances en partant du haut sont 10,40,40)
***image supprimée***
***[edit moderation] : merci de faire l'effort de recopier l'énoncé svp [[désolée pour la perte d'information engendrée Vanoise]]***
Bonsoir
Le règlement du forum demande de recopier l'énoncé et de scanner le schéma. L'énoncé est particulièrement court ici...
L'idée générale consiste à déterminer la tension commune aux trois branches. Le résultat est ensuite immédiat. Cette tension commune peut être obtenue de façon immédiate par le théorème de Milman. Si ce théorème n'est pas à ton programme, tu peux t'en sortir en combinant loi des noeuds et loi d'Ohm.
Daccord je respecterais mieux le reglement pour la prochaine demande et merci pour le renseignement ^^
Pour trouver la tension commune aux trois branches, si tu ne connais pas le théorème de Milman, tu peux commencer par remplacer les résistances en parallèle de 10 et 40
par la résistance équivalente.
Remarque : la question est mal posée : le circuit contient deux résistances de 40 !
Cependant, on obtient une des réponses proposées en considérant qu'il s'agit de la résistance de 40 placée en parallèle avec celle de 10.
Bonjour gbm
[[désolée pour la perte d'information engendrée Vanoise]]***
Aucun soucis. J'ai d'ailleurs signalé le problème à Yazzimani dans mon premier message.
L'énoncé est extrêmement court : sachant :
E1=80V , R2=40
, R3=10 , il s'agit de trouver la valeur de R pour que la puissance dissipée par R2 soit P2=1,6W.
Bonjour ,
Ma part de contribution serait tout simplement d'appliquer le théorème de Millman pour trouver la résistance R sans toute fois oublier Cette relation ( P=UI )
D'après le Théorème de Millman , on a :
U= ;
et aussi U= avec I=
et R'= R+40
De ces relations on trouve R' donc R
D'après le Théorème de Millman , on a :
U=
et aussi U=
De ces relations on trouve R' donc R
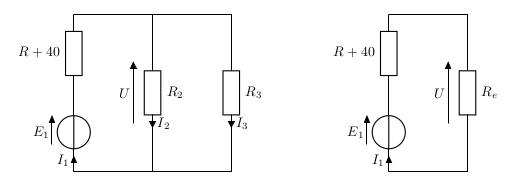
[b]Posons tout d'abord R1=R+40 et Re= R2//R3 d'après le circuit équivalent à gauche on a d'après le PONT DIVISEUR DE TENSION : U=
Annuler
connectez vous