Inscription / Connexion Nouveau Sujet
Egyptiens et pyramides
Voilà l'énoncé de mon DM :
Pour construire les pyramides, les égyptiens ont sans doute utilisé la technique du plan incliné. On donne g=10 N
1° j'ai réussi à répondre
2° idem
3° Des rouleaux de bois, intercalés entre le bloc de pierre et le sol incliné, rendent les forces de frottements négligeables. Pour maintenir le bloc en équilibre et l'empêcher de glisser, un groupe d'homme exerce une force F parallèle à la pente.
a) Faire le bilan de ces forces. On ne demande pas ici les caractéristiques
b) Calculer en utilisant la méthode mathématiques : la valeur de la réaction du support R et la valeur de la force F.
c) Combien d'hommes sont nécessaires pour exercer cette force.
Données : l'angle du support : 20°
Je sèche totalement sur la b. Je ne vois pas comment faire. Je fais une projection mais je ne vois pas à quoi ça mène...
Bonsoir.
Je fais une projection mais je ne vois pas à quoi ça mène...
Et pourtant, c'est bien comme cela qu'il faille procéder... Mais peut-être projetez-vous "mal" ou alors peut-être n'avez-vous pas placé vos axes de manière judicieuse...
Ne sachant rien d'autre sur votre exercice, mais vu que vous êtes en 1ère, on va supposer que la pierre est animé d'un MRU.
Ainsi, les trois forces se compensent telle que
Vous avez donc un schéma dans ce style :
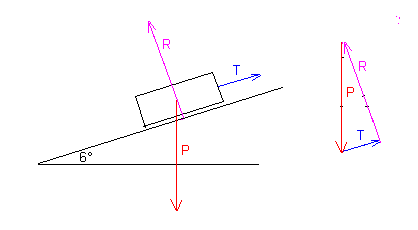
Sauf que c'est 20° au lieu de 6° et qu'il s'agit de
Si vous projetez
 J'appelle
J'appelle Alors vous constatez que
Donc R = Py = m.g.sin(20°) !
(Cours de 2nde)
Par le même raisonnement, afin d'éviter que la pierre ne retombe le long du plan incliné, il faut que
Donc f = m.g.cos(20°)
3c)
Combien d'hommes sont nécessaires pour exercer cette force
Cela dépend de votre énoncé, de quelle force (en N) développe un seul homme !
(Simple proportionnalité !)
- sauf distraction de ma part -
Mon shéma est le même que le vôtre et j'ai fait la projection comme vous le dites ! En fait, c'est seulement la deuxième fois que l'on fait des projections alors je n'ai pas encore de réflexes... Merci beaucoup pour votre aide au moins j'ai compris comment faire !!


