Inscription / Connexion Nouveau Sujet
éclispse solaire (description de l 'univers)
bonjour,
j' ai un problème d'un un exo je 'ai pratiquement rien compris ( la c 'est vraiment trop dure ) quelqu'un m 'expliquer merci
donc voila
La terre trouve à une distance moyenne d=1.50*10 puissance8 km
du soleil , notre étoile.
a).sans souci d 'échelle schématiser la Terre et le soleil ainsi que les deux rayons lumineux qui nous parvient depuis les extrémités du disque solaire.
b)Sachant que le diamètre D du soleil vaut 1.4*10 puissance6 km,exprimer puis calculer l 'angle fi sous lequel un observateur terrestre voit le disque solaire.Exprimer la valeur de cet angle en radian.
c)La lune est le satellite naturel de la terre .Elle se situe à une distance moyenne d' de la Terre égale à 3,84*10 puissance5 km et possède un diamètre D4de 3,4*10 puissance 3km.
Exprimer la valeur de cet angle en radian (c 'est quoi radian?? je ne l 'ai jamais apprise pour le moment.
d)Comparer les angles calculés précédemment.
Quelle conséquences cela peut-il avoir ?
e)Lors d 'une éclipse solaire totale , le disque lunaire occulte le disque solaire.A l 'aide précédent, indiquer comment cela peut être possible
f)Les éclipses solaires totales se produisent peu souvent.
A votre avis quelles sont les raisons de cela ??
J'ai pas mis les réponses car sa fait depuis un bon moment que je travaille sur cet exo et j ai toujours rien compris donc voila c 'est pourquoi j 'aurais bien aimée qu 'on m 'aide un peu et m 'explique !!
Bonjour,
Le radian est une unité qui est utilisée pour la mesure des angles.
Un tour vaut 360° ou 2 radians
radians
360° = 2 rad
rad
Cette égalité te permet de convertir des mesures d'angle en degrés en des mesures d'angle en radians.
Mais sur ta calculatrice tu peux aussi paramétrer les calculs d'angles (pour les sinus, cosinus, tangentes et leurs inverses) en radians.
Question 2 : le calcul d'un diamètre apparent ( ) demande un tout petit peu de trigonométrie. L'un des avantages des radians est que pour de petits angles (ce qui est le cas ici) on peut assimiler la mesure de l'angle en radian avec la tangente ou le sinus de cet angle.
) demande un tout petit peu de trigonométrie. L'un des avantages des radians est que pour de petits angles (ce qui est le cas ici) on peut assimiler la mesure de l'angle en radian avec la tangente ou le sinus de cet angle.
 (rad)
(rad)  tan(
tan( )
)  sin(
sin( ) pour de petits angles !
) pour de petits angles !

merci pour l information
mais cependant j ai toujours pas compris 
j 'ai vu sur un site que l 'on pouvait calculer comme sa (enfin je crois)avec cette formule
360*14/29-2fi=180° (c 'est bon sa ???)
comme j ai pas compris pourquoi il y a 14/29 et 2*fi donc je voudrai comprendre svp si vous voulais bien m expliquer
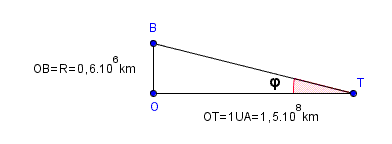
Dans la figure précédente (qui n'est évidemment pas à l'échelle) :
O représente le centre du Soleil
B représente un bord du Soleil
OB = rayon du Soleil (la moitié de son diamètre)
T représente la Terre
OT : représente la distance moyenne de la Terre au Soleil, c'est-à-dire une UA
J'ai écrit  pour l'angle. Il aurait été préférable que j'écrive
pour l'angle. Il aurait été préférable que j'écrive  /2 car l'angle que j'ai représenté vaut la moitié du "diamètre apparent" du Soleil vu de la Terre.
/2 car l'angle que j'ai représenté vaut la moitié du "diamètre apparent" du Soleil vu de la Terre.
Je me suis également trompé dans le calcul du rayon du Soleil... 
Bon, je recommence l'image :
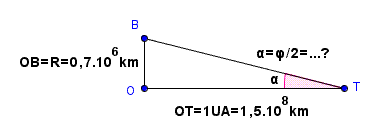
Que vaut la mesure de l'angle 
et, en conséquence,
que vaut le diamètre apparent du Soleil,  vu de la Terre ?
vu de la Terre ?

et bien tan fi=0b/0t
tan fi= 0.6.10^6/1.5.10^8
tan fi=1/250
tan-1(1/250)
= a peu prés 0.23°
en radian sa donne peut être sa 0.23*2*pi
=1.45rad
bon je recommence les calcules
et bien tan fi/2=0b/0t
tan fi/2= 0.7.10^6/1.5.10^8
tan fi/2=1/250
tan-fi=(1/250)/2
= a peu prés 1.34°
en radian sa donne peut être sa 67/25*pi
=8.42 rad

tan( ) = OB / OT = 0,7.106 / 1,5.108
) = OB / OT = 0,7.106 / 1,5.108  0,004 67
0,004 67

 tan-1(0,004 67)
tan-1(0,004 67)  0,267°
0,267°

 0,267
0,267  2
2 / 360
/ 360  0,004 67 rad
0,004 67 rad
 = 2
= 2 
 0,009 3 rad
0,009 3 rad
________________
Si tu étudies bien ce qui est écrit ci-dessus, tu constates que l'on pouvait utiliser la relation (valable pour les petits angles) selon laquelle :
tan( )
) 
 rad
rad
et il n'y a plus besoin de faire une conversion.
________________
Maintenant que tu as vu comment faire pour la question b (le Soleil vu de la Terre) tu sais comment faire pour la question c (la Lune vue de la Terre). A toi !

j 'ai pris le même triangle j 'ai remplacé le rayon du soleil par celui de la lune ,d 'ou lb=1700
tan(fi)=lb/lt =1700/3,84*10^5 égale a peut prés.00443
(fi) et égale a peut prés tan-1(0.00443)égale a peut prés0.254°
(fi)égale a peut prés0.0;254*2*pi/360égale a peut prés0.00443 rad
(fi)=2*0,00443=0,0087rad
donc la lune vue de la terre est de 0,0087 rad
Bien !
Attention, ne mélange pas  et
et  ! Tu calcules d'abord
! Tu calcules d'abord  (en utilisant un rayon du Soleil puis de la Lune) puis tu le multiplies par 2 pour avoir
(en utilisant un rayon du Soleil puis de la Lune) puis tu le multiplies par 2 pour avoir  qui est le diamètre apparent.
qui est le diamètre apparent.
Personnellement, quand je fais le calcul, j'arrondis à 0,008 9 rad
Vois-tu qu'ici encore tu aurais pu éviter de passer par les degrés. Dès que tu avais calculé tan( ) tu pouvais multiplier le résultat par 2 et ainsi tu avais la valeur de
) tu pouvais multiplier le résultat par 2 et ainsi tu avais la valeur de  en radian.
en radian.
A toi pour la suite !

l angle de la lune vue de la terre est plus petit que que l 'angle vu du soleil
donc est ce que je px faire sa
le rapport de l angle du soleil sur celui de la lune ???
C 'est à DIRE 9,3*10¨-3/8,9*10¨-3=1.04
comment met t-on 1.04 en pourcentage ???
Ces deux angles sont presque égaux.
1,04 peut s'écrire 104 %
Avec les valeurs de l'énoncé, si la Lune est juste devant le Soleil, l'éclipse n'est pas totale puisque le diamètre apparent du Soleil est supérieur à celui de la Lune. On a alors une "éclipse annulaire" : la lumière du Soleil dessine un anneau autour de la Lune.
Pour que l'éclipse soit totale (ce qui est un évènement rare) il faut non seulement que la Terre, la Lune et le Soleil soit alignés, mais il faut aussi que la Lune soit plus proche de la Terre que la valeur moyenne donnée par l'énoncé (et les variations de la distance de la Lune à la Terre sont assez importantes) et c'est encore mieux si la Terre est un peu plus loin du Soleil (mais cela ne varie pas tellement).
Enfin, même quand une éclipse totale peut avoir lieu, cela ne sera visible que de peu d'endroits de la Terre (il y a des personnes qui ne rateraient ce spectacle pour rien au monde et qui font de grands voyages pour se trouver là où il l'éclipse sera visible). Le diamètre de la Terre est plus important que celui de la Lune et la presque égalité des diamètres apparents fait qu'il faut vraiment se trouver sur la droite qui passe par le centre du Soleil et par le centre de la Lune. Si l'on s'éloigne de cette droite l'éclipse est partielle et n'est plus totale.
Je pense qu'avec cela tu peux essayer de répondre aux dernières questions.

vous savez pour la question b et c mon prof il la faite d'une autre manière
il a fait alfa=2*tan-1(Diamètre/2*distance)
mais cependant grâce à vos explications j ' ai mieux compris !!!
Une autre manière ? Pas vraiment :
Le rayon R est la moitié du diamètre D
R = D / 2
et d'autre part  = 2
= 2 
En notant d la distance de la Terre à l'astre considéré
 = tan-1(R / d) = tan-1[D / (2 d)]
= tan-1(R / d) = tan-1[D / (2 d)]
 = 2 tan-1[D / (2 d)]
= 2 tan-1[D / (2 d)]
Mais puisque l'on cherche la valeur en radian d'un petit angle il faut poursuivre :

 D / d
D / d
______________
Je t'en prie.
A une prochaine fois !