Bonjour, j?ai un dm à la rentrée, et je voudrais savoir si mes réponses sont justes, voici l?énoncé ;

L?or cristalline en réseau cubique a face centrée. Les atomes d?or sont assimilés à des sphères rigides, tangentes entre elles, de rayon r, : 144,2 pm (1pm=10^-12). Les points de tangence sont situés sur la diagonale d?une face du cube. Ci-contre la représentation plane de la face d?une maille ( les  points représentant la position des centres des atomes d?or ) ; a est la longeur de l?arrête de la maille et le rayon d?un atome.

1) Démontrer par le calcul que a= 407,9pm.

Donc a= 4R/(racine)2= 4x144,2/(racine)2= 407,9 pm
Le volume totale du cube est donc 407,9 pm.

2) En deduire le volume d?une maille cubique en pm au cube.

a( au cube ) = (4R/racine de 2) au cube =
8445638,1 pm ( au cube )
Le volume d?une maille est 8445638,1 pm au cube.

3) Le volume d?une sphère de rayon étant V= 4/3xxr( au cube ), retrouver la compacité au cristal d?or.

Ccfc= 4x4/3(r)au cube / ( 4/ ( racine )2 au cube = 4x4(144,2 au cube ) / (4x144,2/( racine) 2)au cube = 2,2 %

Donc 2,2 % est le volume du cube occupés par les atomes.

Merci, et bonne soirée à vous !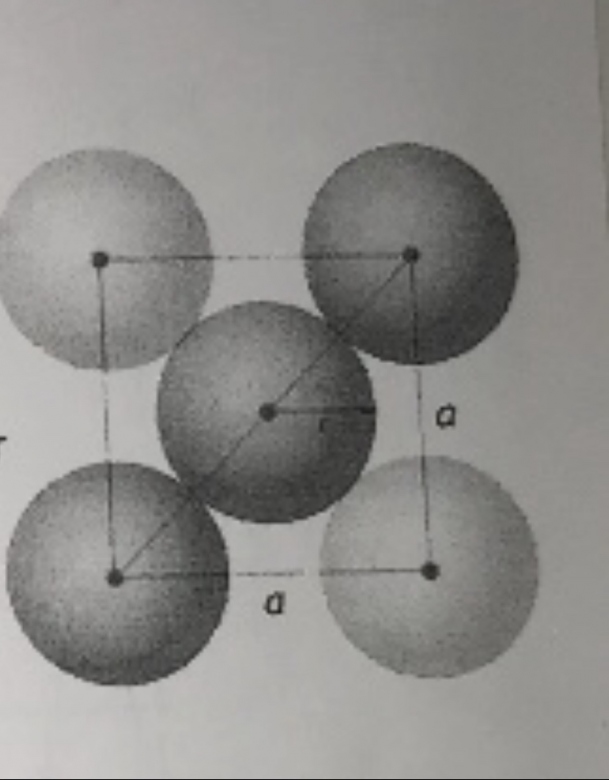



***Titre complété pour plus de clarté***