Inscription / Connexion Nouveau Sujet
DM Montagne russe énergie physique
J'ai un dm à rendre pour ***échéance supprimée*** mais je suis bloqué, veuillez m'aider s'il vous plait.
Le wagon subit des actions mécaniques liées aux rails modélisées par une force de frottement f supposé constante. On admet que son travail sur une portion curviligne de façon identique à portion rectiligne du circuit. On néglige l'action de l'air.
Données: Longueur de la piste: AB=120m ; masse du wagon: m=500kg ; f=600N.
LE PROBLÈME À RÉSOUDRE: Quelle doit être la vitesse minimale en A pour que le wagon parcourt la totalité de la boucle avec une vitesse supérieure à 20 km/H ?
Mes pistes:
Je pense que je doit calculer l'énergie mécanique au point et au point B pour ensuite trouver la vitesse.
Em(A)= Ec(A)+ Epp(A)
=1/2mv^2+mgh
Em(B)=Ec(B)+Epp(B)
=1/2mv^2+mgh'
Je pense que va doit être supérieur à 20 km/h peut être avec une inéquation?
Or je ne sait que faire après avec la longueur AB et les forces frottement ou f=600.
Merci 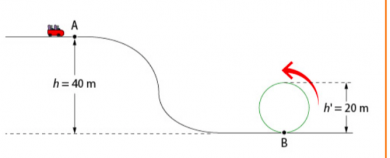
***Image recadrée****
Bonjour,
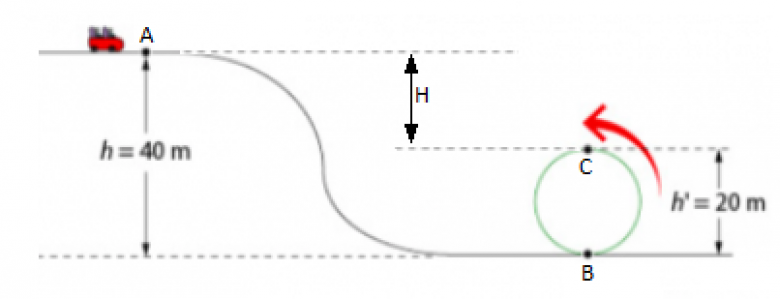
Ce n'est pas au point B, mais au point C diamétralement opposé à B que la vitesse du wagon est la plus faible.
Je suggère d'appliquer le théorème de l'énergie cinétique entre les points A et C en supposant que la vitesse du wagon au point C est égale à 20 km/h.
bonjour donc :
deltaEc= Wab(vect F ext )
Ec(C) - Ec(A) = Wab(vectP)+ Wab(vectR) + Wab(vect F)
Or les travail des forces modélisant l'action de la Terre et la réaction du support sont nuls.
Ec(C)- Ec(A) = F x AB
1/2mV(c)^2 - 1/2mV(a) = Fx B
1/2X500X20^2 - 1/2 mV(a)^2 = FxB
V(A)^2= (2xFxAB+100 000)/m
V(A)^2 =(2x600x120+ 100 000)/m
V(A)^2= 88
V(A)= rac 88= 9,4 m/s (=35 km/h)
Est-ce cela ?
Merci
deltaEc= Wab(vect F ext )
Ec(C) - Ec(A) = Wab(vectP)+ Wab(vectR) + Wab(vect F)
Jusqu'ici tout va bien !
Or les travail des forces modélisant l'action de la Terre et la réaction du support sont nuls.
Mais ici ça se gâte ....
S'il est vrai que le travail de la réaction du support (qui est sans cesse perpendiculaire à la direction du déplacement) est nul il n'en est pas de même pour le travail du poids.
Ec(C)- Ec(A) = F x AB
Et ici tu n'as pas tenu compte que les forces de frottement font un travail résistant sans compter que ce n'est pas sur AB que le wagon se déplace, mais sur AC.
effectivement donc:
Ec(C)-Ec(A)= Wac (vect Fext)
=Wac(vectP)+ Wac(vectR)+Wac(vectF)
=mgxACxcos (180)+ RxACxcos(90)+ F
=-Px AC
= -F XAC
Je suis un peu perdu je crois
J'ai l'impression que tu ne sais pas calculer le travail du poids ( A revoir donc ....)
Théorème de l'énergie cinétique entre A et C :
avec :
Je pose h-h' = H
Je pose L = longueur du trajet ABC
Je te laisse continuer.

 1,5m/s
1,5m/s

