Inscription / Connexion Nouveau Sujet
DM Epp
Bonjour, j'espère que vous allez bien ?
Alors voilà, je suis un peu perdu dans ce dm de physique, je ne vois plus trop comment avancer....
Tout d'abord, l'énoncé intégrale de l'exercice :
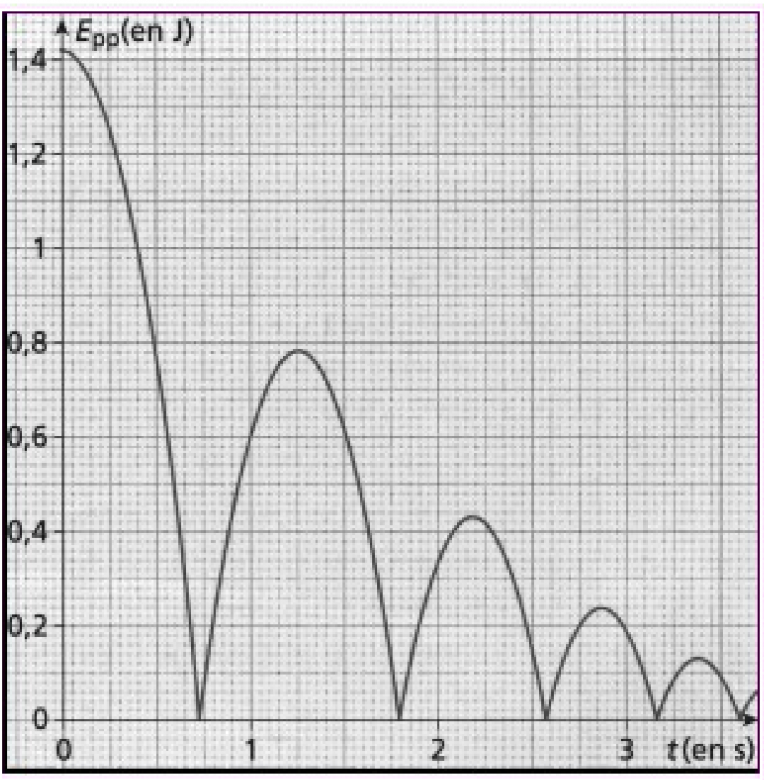
La courbe suivante représente l'énergie potentielle de pesanteur d'une balle de tennis
de masse m=57 g lâchée sans vitesse initiale d'une hauteur z0 au dessus du sol. On choisit le niveau
du sol comme origine des altitudes z=0.
1) A quelle date la balle touche-t-elle le sol pour la première fois ? Justifier.
2) A l'aide de la courbe et d'un calcul, déterminer l'altitude initiale z0 de la balle.
3) A quelle date t1 la balle atteint-elle son altitude maximale après le premier rebond ?
Calculer l'altitude z1 correspondante.
La balle est-elle conforme aux spécifications selon lesquelles « Le rebond d'une balle tombant
d'une hauteur de 254,00 cm sur une surface plane et dure (en béton par exemple) doit être au mi-
nimum de 134,62 cm et inférieur à 147,32 cm » ?
4) En supposant les frottements négligeables lorsque la balle est en l'air, déterminer l'énergie mé-
canique Em0 de la balle avant son premier rebond.
5) A la date t1, que vaut l'énergie cinétique de la balle ? Justifier.
6) En déduire la valeur de l'énergie mécanique Em1 de la balle entre son premier rebond et son
deuxième rebond ?
7) Quel pourcentage de l'énergie mécanique a été perdue lors du rebond ?Sous quelle forme ?
8) Compléter le graphe en ajoutant d'une couleur l'énergie cinétique EC et d'une autre l'énergie
mécanique Em .
1) j'ai mis ≈0,75 seconde, car nous pouvons voir clairement sur la courbe que c'est son premier rebond.
2) c'est la que je suis embêtée, car je pense qu'il faut utiliser Epp= m*g*z
En la retournant tel que z= Epp / (m*g)
Mais le problème, c'est que je n'ai pas l'énergie potentielle de pesanteur
Merci de votre aide 👍
Bonjour,
Question 2 :
Il me semble bien pourtant que l'énergie potentielle de pesanteur se lit directement sur la courbe !
Ok, mais je prends qu'elle valeur ? Celle à la position initiale, c'est à dire ≈ 1,4 ?
Sinon pour la question 1, c'est bon ?
Question 2 :
Oui,
L'énoncé demande l'altitude initiale de la balle laquelle correspond à l'énergie potentielle initiale soit 1,42J et non ( 1,4 sans la moindre unité ! ! ! )
Question 1 :
J'ai trouvé  0,725s
0,725s
Question 2 :
Ton calcul : z0 = Epp(0) / (m*g) est exact
Et ton application numérique : est bien posé.
Mais le résultat que tu obtiens (2,5µm) est invraisemblable.
D'après ce résultat l'altitude initiale de la balle serait du même ordre de grandeur que celle de la taille d'une bactérie !
A revoir donc ...
J'ai du faire un erreur de convers(at)ion, je ne sais jamais si c'est 10^-3 ou 10^3
Ta conversion 57g = 57.10-3 kg est exacte.
Ce n'est pas une erreur de conversion.
C'est une erreur de calcul.
Cela arrive à n'importe qui, mais ce qui est anormal c'est de ne pas se rendre compte que le résultat est parfaitement invraisemblable.
Le résultat du calcul est 2,54m ( et pas 2,5 sans aucune unité )
On est donc bien loin du résultat que tu avais trouvé (Voir ton post du 23-02-20 à 20:21) qui était 2,5.10-6 m c'est à dire un résultat invraisemblable puisque un million de fois trop petit
Je suppose que ton T1 correspond en réalité au t1 de l'énoncé.
Si c'est bien le cas, ton résultat est faux puisque t1 est la date à laquelle la balle atteint son altitude maximum (après le premier rebond)
Il y a une seconde raison pour laquelle ton résultat est faux : Il est totalement dépourvu de sens puisque rendu sans unité.
Mais la date est elle différente du temps ?
(Au tant pour moi, j'ai inversé mes deux axes quand j'ai pris la mesu
t1 = 1,25s est en effet la réponse correcte.
Pour répondre à ta question, il ne faut pas confondre une date avec une durée.
La durée est la différence entre deux dates.
Exemple :
Le premier rebond débute (approximativement) à la date 0,75s
Il se termine (toujours très approximativement) à la date 1,75s
La durée de ce rebond est égale à 1,75 - 0,75 = 1,0s
J'évite l'emploi du mot "temps" qui peut être mal interprété (soit comme une date, soit comme une durée entre deux dates)
Elle a été lâchée de 254,00 cm
Elle a rebondi à une hauteur min de 134,62 cm et inférieure à 157,32 cm
La balle a en effet été lâchée d'une hauteur de 2,54 m comme cela a été démontré.
Voir question 2 et sa réponse (27-02-20 à 23:05)
Elle a rebondi à une hauteur de 1,40 m comme cela a été également démontré.
Voir question 3 et sa réponse (29-02-20 à 17:39) et (29-02-20 à 18:32)
On est donc en mesure en confrontant ces résultats aux conditions stipulées par l'énoncé de décider si cette balle est oui ou non conforme à ces stipulations.
Pour la question 4, peut-on calculer l'énergie mécanique sans l'énergie cinétique ?
Pour pouvoir la déduire après
Sinon, pour la vitesse, on prends la vitesse initiale, vue que c'est avant le 1er rebond donc 0 ?
Cela me paraît étrange
Peux tu trouver l'énergie mécanique au départ de la balle à l'instant où elle est lâchée sans vitesse initiale ?
Si la réponse est "oui" alors tu as la réponse à cette question 4 car (vu l'absence de frottements) entre son départ et juste avant son premier rebond l'énergie mécanique de la balle reste constante.
C'est à dire que connaître son énergie mécanique à l'instant initial c'est aussi connaître son énergie mécanique pendant toute la durée de cette phase.
4. Si les frottements sont négligeables lorsque la balle est en l'air, on peut dire que
l'énergie mécanique E0 de la balle avant son premier rebond se conserve.
On peut alors écrire E0 = Ec0 + Epp0 = Constante et comme à la date t = 0 s Ec0 = 0 car le balle est lâchée sans
vitesse initiale, on a E0 = Epp0 = 1,42 J.
5. L'énergie cinétique de la balle a pour expression Ec = (1/2)*m*v²
À la date t1 Epp1 = Eppmax et E c = 0 donc comme l'énergie mécanique se conserve entre
deux rebonds : E1 = Epp1 = 0,78 J.
Question 4 :
Exact : Avant son premier rebond l'énergie mécanique de la balle est en effet égale à 1,42J
Question 5 :
La question porte sur l'énergie cinétique de la balle à la date t1 = 1,25s
A cette date la balle atteint son altitude maximale (après le 1er rebond) sa vitesse devient nulle. Son énergie cinétique est donc nulle elle aussi.
Tu as plus ou moins déjà répondu à cette question 6 (dans ta réponse à la question 5)
Entre les dates 0,75s et 1,25s l'énergie mécanique reste constante.
Que vaut elle ?
Mais oui !

J'en profite pour compléter mon dernier post qui disait qu'entre les dates 0,75s et 1,25s l'énergie mécanique restait constante (ce qui reste vrai !)
En fait, j'aurais du écrire que c'était entre les dates 0,75s et 1,75s qu'elle restait constante.
A la date t=1,25s l'énergie cinétique est nulle, l'énergie potentielle est égale à 0,78J, donc l'énergie mécanique est aussi égale à 0,78J et comme cette énergie mécanique reste constante, elle garde cette même valeur de 0,78 J entre les dates 0,75s et 1,75s


