Bonjour, j'ai pour demain un DM de physique est je bute sur quelques questions. C'est un exercice aidé avec des réponses partielles mais pour être précise c'est 2 questions qui me posent problème.
J'écris l'énoncé ainsi que ce que j'ai déja fais :

Un grain de sel
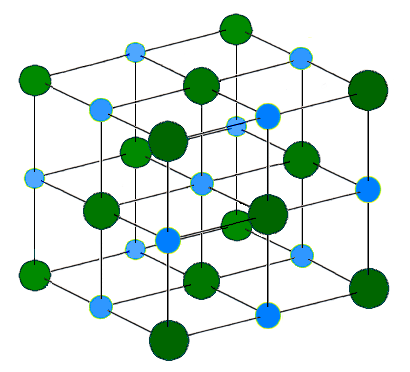
Le cristal de chlorure de sodium est constitué d'un empilement ordonné d'ions. Les ions Cl- se trouvent aux sommets des cubes contigus d'arête a et au centre de chaque face de ce cube ; les ions Na+ sont situés au milieu de chaque arête et au centre de chaque cube.

Schéma de la struture du cristal de chlorure de sodium.
Bleu : Na+
Vert : Cl-
Distance d'un arête : a
Données : a = 556pm ; e=1,6 x 10(-19); k=9 x 10(9)SI

1. Calculer la plus petite distance entre :
a) un ion Cl- et un ion Na+
b) deux ions Cl-
c) deux ions Na+

C'est la question c) (surtout) qui me pose problème mais j'aimerais avoir une confirmation pour la b).
En effet pour la b) il me donne comme réponse patielle (ce que j'ai mis qui ne figurait pas dans la réponse partielle est en gras) :

b) La plus petite distance entre deux ions Cl- est celle qui sépare un ion Cl- placé à un sommet d'un cube et l'ion Cl- placé au centre d'une face. La diagonale d'un carré de côté a vaut 1/2a (j'aimerais savoir comment justifier précisément ma démarche) La distance entre deux ions Cl- les plus proches est donc égale à : 1/2a = 1/2 x 556 = 556/2 = 278 pm = 2,78.10(-10)m (je retrouve le même résultat que pour la question a) donc je ne sais pas si c'est juste ...)

c) Par symétrie .... C'est ici que je suis bloquée je ne vois pas comment je pourrais continuer la démarche pour arriver au résultat.

Merci d'avance