Inscription / Connexion Nouveau Sujet
dm de math
salut j'auai besoin d'aide pour mon dm de math
On considère un ressort de longueur initiale lo = 10 cm. On étire ce ressort de 2 cm , puis on le lache à l'instanr x = 0s . Le ressort se met alors à osciller autour de sa position d'équilibre et l'on admet que sa longueur l(x) est donnée par l(x) = 10+2cos(
x) (en cm) ou x est le temps (exprimé en secondes)
a ) determiner les instants x en lequels le ressort repasse par sa position d'équilibre ( c'est _à-dire les réels x
0 pour lesquels on a lx) = lo )
b ) parmi tous ces instants , déterminer ceux qui sont compris entre 0s et 5s .
c ) Determiner les instants x en lequels la longueur du rressort est égale à 11 cm
d) parmi tous ces instants, déterminer ceux qui sont compris entre 0s et 5s
j'ai vraiment besoin d'aide je ne sais pas comment procéder
merci d'avance
Bonjour,
Cette image n'est pas la solution, mais elle devrait te mettre sur la piste des réponses :
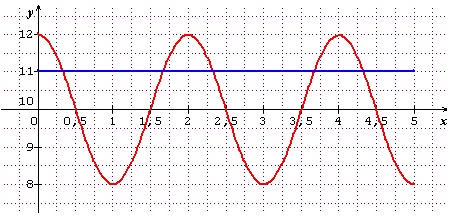
A toi ...
oui j'ai cette image mais il faut répondre au question par calcul et je ne sais pas comment procéder
l(x) = l0 + 2 cos( x)
Pour quelles valeurs de x a-t-on
l0 + 2 cos( x) = l0
Et donc pour quelles valeurs de x a-t-on
cos( x) = 0 ?
j'ai trouvé
l(x)= lo
l(x)= 10
10+2cos(x) = 10
2cos(x) = 0 On sait que cos /2) = 0
c'est-à-dire (cosx) = cos (/2)
(x)
/2 mod[2]
avec k 
ztel que
x = /2+2k
x = /2
1/+2k/2
x = 1/2 + 2k
ou (x) 
[/smb]/2 mod [2]
avec k'z tel que
x=-/2+2k'
x = - /2 + 1/ + 2k'/2
x = -1/2 + 2k'
Attends, avant la question c il y a la question b
Oui, pour la question c il faudra procéder de la même manière.
Annuler
connectez vous