Inscription / Connexion Nouveau Sujet
Diminution d'un ressort
Bonjour
J'aurais besoin d'aide pour cet exercice :
Chapitre : énergie mécanique.
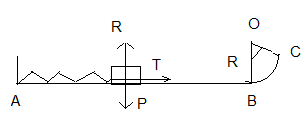
AB est horizontal, BC est un arc de centre O et rayon R.
La gouttière se trouve dans un plan vertical , les points O et B se trouvent sur la même verticale .
Un solide de masse m peut être lancé de A par intermédiaire d'un ressort de raideur K .
1. Trouver la diminution minimale de longueur l0 qu'il faut imprimer au ressort pour qu'il puisse envoyer le solide jusqu'en C.
On donne:
m= 100g ; R=0,5m; 
= 60°; K= 10N/m.
2. On imprime maintenant au ressort une diminution de longueur 2l0.
Trouver la vitesse du solide au passage par le point C
Ma réponse:
-1/2 mV2 1/2. J
W2= mgh+T.AC
ça ne marche pas ?
Merci d'avance 
Bonsoir,
Je ne comprends rien à ta formule...
Il faut faire ça par l'énergie...
L'énergie cinétique au point B est transformée en énergie potentielle (avec énergie cinétique nulle en C).
L'énergie cinétique de la masse m est égale à l'énergie fournie par le ressort.
bonsoir beugg.
Arriver en c veut dire que vc>=0, appliquer thm de l'energie cinetique 1/2(vc2-vb2)=
.
.
vb>=-2./m.soit D le point où le corps est laché alors AD=longueur du ressort,soit l0 la longueur de ressort comprimé . si entre D est B le mvt s'effectue sans frottement alors vd=vb car le poids ne travaille pas. Le thm de EC durant la compression de ressort 1/2mvd2-0=
kx.dx 1/2mvb2= 1/2k(l2-l0).L connaissance de l est nécessaire .Cela est une aide !!
bon courage.
Bonjour à tous
Pour le théorème Ec durant la compression, je ne comprends pas l'expression que donnait Alhassan.
Quelqu'un pourrait m'expliquer si Aragorn et Alhassan se sont occupés
L'énergie potentielle d'un ressort étiré ou comprimé est égale à :
k étant la constante de raideur du ressort et x est la différence de longueur par rapport au repos (x = l0 - l ).
C'est cette énergie potentielle qui se transforme en énergie cinétique pour la masse lorsque le ressort a fini de la pousser...
V= omega*R ... Oui, mais ça ne nous sert pas ici...
Ce que l'on cherche, c'est la vitesse sur la partie plate du trajet. L'énergie potentielle du ressort () est transformée en énergie cinétique pour la masse m. La vitesse reste constante (pas de frottement) et l'énergie cinétique aussi.
Sur la partie courbe, l'énergie cinétique est transformée en énergie potentielle de pesanteur. L'énergie mécanique reste constante. En B, l'énergie mécanique est l'énergie cinétique (pas d'énergie potentielle) et en C, l'énergie cinétique est nulle (pour la première question) et l'énergie potentielle de pesanteur est mgh.
Donc, on a :
Ou, en reprenant les notations de l'exercice :
avec :
Bonjour Aragorn
Ok c'est très clair
Donc x= 0,22 m
Pour la question 2,
Que veut dire: la diminution de longueur2l0 ?
Pour la question 2
On comprime le ressort d'une longueur 2l0 (l0 étant la réponse à la 1ère question).
L'énergie potentielle du ressort est alors :
L'énergie mécanique au point C est :
Donc :
D'où ...
D'accord Aragorn
Avant de vous laisser
Donc quand on transforme une énergie en autre énergie ça veut dire que : ces deux énergies sont égales?
Je ne comprends pas bien concernant les transformations
merci de m'expliquer
Oui, on peut dire que ces deux énergies sont égales.
L'exemple le plus simple est la chute libre. On a une masse m à une hauteur h. Son énergie potentielle est et son énergie cinétique est nulle. Son énergie mécanique est donc égale à son énergie potentielle.
Lors de la chute, l'énergie mécanique reste constante si on néglige les frottements. Progressivement, l'énergie potentielle diminue et l'énergie cinétique augmente. On peut dire que l'énergie potentielle se transforme en énergie cinétique. Arrivé au sol, l'énergie potentielle est nulle et l'énergie cinétique est maximale. L'énergie cinétique est alors égale à l'énergie potentielle initiale. On peut dire que l'énergie potentielle s'est transformée en énergie cinétique.
Annuler
connectez vous