Inscription / Connexion Nouveau Sujet
Devoir sur les forces
Bonjour, j'ai un devoir en physique a faire.
Cependant , j'ai rencontré quelques petit problèmes au niveau de la crétion du schéma.
Merci beaucoup de m'aider =)
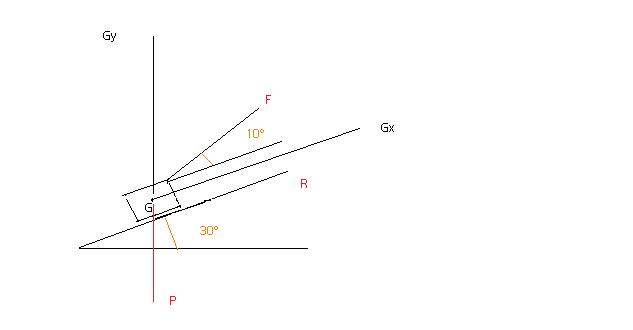
Un solide S de masse m = 50kg est posé immobile sur un plan incliné faisant un angle alfa = 30° avec l'horizontale.
Ce solide est retenu par un fil faisant un angle de Beta= 10° avec le plan incliné.
Il n'y a pas de frottement entre le plan et le solide.
1) Faire le bilan des forces appliqués au solide et indiquer la relation vectorielle qui les relie.
2) Methode analytique :
-Soit le repère ( Gx, Gy ) tel que l'axe Gx soit parallèle au plan incliné, orienté vers le haut du plan, et l'axe Gy orienté vers le haut.
-Représenter les vecteurs-force et exprimer( littéralement) leurs coordonnées dans ce repère.
-Déterminer( expression littérale, puis calcul numérique ) la veleur de la tension fil et celle de la réaction du plan sur le solide S.
Merci =D 

Bonsoir, cet exo est une application du cours...
Ce n'est pas à nous de le faire ! Tu postes tes réponses et je te corrige.
1) bilan des forces appliqués
- action de la terre  P
P
sens : vers le bas
direction : verticale
pts d'application : centre de gravité
valeur : P=m.g, P=9.8*50= 490 N
- action du plan  R
R
sens : vers le haut
direction: horizontale
pts d'application: surface de contact
-action du Fil :  F
F
sens: vers le haut
direction: verticale
pts d'application : point de contact .
2)je n'arrive pas a faire le repère et je doute pour les coordonnées de F .
coordonnées:
P (Px, Py) R(Rx,Ry) F(Fx, Fy)
P (0, -P ) R(R*SIN(X) , R*COS(x)) F(F*Sin(x),F*COS(x))
Ps: dans votre figure , le fil ne fait pas 10° avec le plan incliné.
L'angle se trouve de l'autre coté.
1) bilan des forces appliquées
- action de la terre P
sens : vers le bas
direction : verticale
pts d'application : centre de gravité
valeur : P=m.g, P=9.8*50= 490 N
TB
- action du plan R
sens : vers le haut non ! elle est perpendiculaire au plan
direction: horizontale non!
pts d'application: surface de contact oui
-action du Fil : F
sens: vers le haut NON ! Elle a le sens du fil !
direction: verticale
pts d'application : point de contact .
Complète mon schéma :
- place-y le repère
- place-y les forces
Non la réaction du support, s'il n'y a pas de frottement est perpendiculaire à Gx.
Je reviens + tard
c'est vrai.
Donc R doit etre perpendiculaire a Gx et doit passé par G.
Donc R est sur Gy.
Et R = Rn (reaction normale)
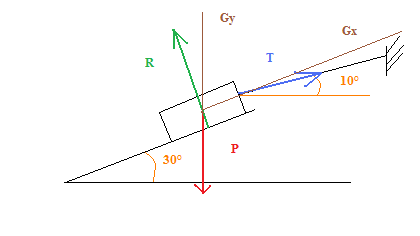
G(Gx,Gy)
P(-P.sin 30° ; -P)
R(0 ; R.cos 30°)
T( T.cos 20° ; T.cos 80°)
sauf erreur.
Un conseil : place tous les angles qui vont être utiles.
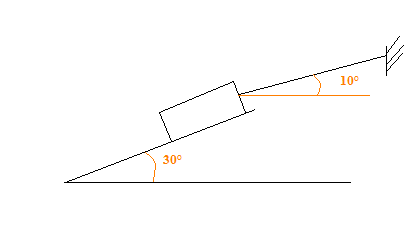
Le profeseur nous a donné un schéma qui correspond a celui ci dessous.
sans le repères et vecteurs .
P( -p * sin(30); -P)
R( ; cos(30))
D'après ce qu'on voit, R ne part pas de 0 qui est le ponit g , mais pas de la surface du solide S.
Je n'arrive pas a determiné Rx et T
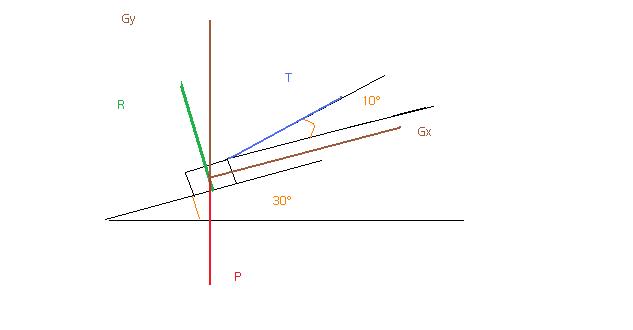
Pas tout a fait.
Dans votre figure, on par du milieu d'un coté du solide pour T et l'angle est en bas de la droite.
Tandis que dans le cas normal, on part d'un segment et l'angle est au dessus de la droite .
Mais on ne peut pas calculer les coordonnées de T et R. Car il nous manque des indications.
Pas tout a fait.
Dans votre figure, on par du milieu d'un coté du solide pour T et l'angle est en bas de la droite.
Tandis que dans le cas normal, on part d'un segment et l'angle est au dessus de la droite .
en même temps, tu ne m'avais pas donné le point d'application de la corde. Mais cela ne change rien à la force T.
Mais on ne peut pas calculer les coordonnées de T et R. Car il nous manque des indications.
Je l'ai bien fait au-dessus. A vérifier

En effet, j'ai fait une erreur. J'ai fait le calcul pour un angle de 20° au lieu de 10°...
Dans ce cas la projection du vecteur T sur les axes est
/Gx : T.cos 10°
/Gy : T.cos 50°
sauf distraction
coordonées :
P(-P.sin 30° ; -P)
R(0 ; R.cos 30°)
T ( T.cos 10° ,T.cos 50° )
normalement , c'est pas sin(10°)
D'après le principe d'inertie
P+R+F = 0
donc
Px + Rx + Fx = 0
-p.sin(x) + 0 + t.sin(x) = 0
(-p+t)sin(x) = 0
normalement , c'est pas sin(10°)
pourquoi ? Quel est l'angle entre T et Gy ?
D'après le principe d'inertie
P+R+T = 0
TB !
Tu utilises cette relation avec les projections faites auparavant : elle devient
/Gx :
/Gy :
J'ai fais uen erreur. Je croyais que c'etait le coté opposé.
0 = Px + Tx + Rx
0 = -p sin(x) + t.cos(x) + 0
0 = -p sin(x) + t.cos(x)
0 = -490.sin(30) + t.cos(10)
0 = 484 + t*0.83
-484/0.83 = t
-576 N
Il doit y avoir un problème
0 = Py +Ty +Ry
0 = -p + R.cos(30) + T cos 50
0 = 490 N + Rcos 30 + T cos 50
(P+ t.cos50)/ ( cos 50 ) = R
Houlà,
pouruoi un x dans cos et sin ?
un T devient t ...
0 = Px + Tx + Rx
0 = -Psin30 + Tcos(10) + 0
soit T = Psin30°/cos10°
Dans
0 = Py +Ty +Ry
0 = -P + Tcos 50° + Rcos30°
T est connu de l'ancienne relation
donc R = (P-Tcos50°)/cos30°
sauf erreur 
il y a une grande différence .
T = Psin30°/cos10°
T = 490*sin(30) / cos(10)
T = 490*0.50 / 0.99
T= 249 N
R = (P-Tcos50°)/cos30°
R = 490-249*0.65 /0.86
R = 381 N
ma calculatrice est en mode radian .
Merci beaucoup pour votre aide =D