Inscription / Connexion Nouveau Sujet
defi physique
Bonjour,
un de mes professeur m'a proposé un défi a relever en physique. il m'a dit qu'il fallait utiliser le tuyau sin(A-B)= sinA*cosB-sinB*cosA.
Malgré cela je n'ai pas utiliser cette formule mais je suis arriver a une réponse mais il parait qu'elle est fausse.
J'ai photographié le défi, voila le lien: 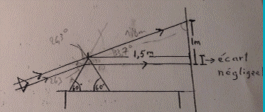
** énoncé effacé ; image laissée **
merci beaucoup
Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum 
![]()
Bonjour,
Quelle valeur as-tu trouvée ?
Connais-tu la bonne valeur ?
Poste l'énoncé ! Il est intéressant et sort de l'ordinaire.

Oui j'ai biensur fait de l'effort, vous le voyez bien sur la photo.
D'abord j'ai trouvé que l'angle d'incidence au tout début était de 63,7 et le dernier Ngle de réfraction est de 30. Ce que je cherche , c'est l'indice de réfraction du prisme.
J'ai fait sin63,7 x 1 = sink x n
Sint x n = sin30 x 1
Donc. Sin63,7 / sink = n = sin30 / sint
=> sin63.7 / sin30 = n = 1,79
Cependant, mon prof m'a dit qu'il fallait utiliser le tuyau sin(A-B)= sinA*cosB-sinB*cosA, sinon on n'arriverait j'aimais à la bonne réponse.
Aidez moi svp
Défi intellectuel:
Un prisme triangulaire équilatéral repose sur une table horizontal. Le sommet supérieur du prisme se trouve à 1.5m d'un mur vertical. On dirige un faisceau lumineux vers ce sommet supérieur avec un certain angle d'incidence. Le pinceau se scinde alors en deux parties, une des parties continue sont chemin dans sont orientation initiale ( sans déviation ) et l'autre se réfracte et ressort du prisme parallèlement à la table. Si les deux parties du pinceau aboutissent sur un mur et que les deux rayons sont éloigné de 1 m, qu'elle est l'indice de réfraction du prisme?
Il y a beaucoup de bonnes choses, mais pas la fin.
Je suis tout à fait d'accord avec les valeurs suivantes :
i  63,69°
63,69°
i' = 30°
Pour utiliser les notations habituelles je poserai également :
sin(i) = n.sin(r)
et
sin(i') = n.sin(r')
Comment continuer ?
Il faut que tu cherches, par la géométrie une relation entre les angles r, r' et A ; trois angles qui sont à l'intérieur du prisme.
Quand tu auras cette relation tu pourras remplacer r' en fonction de r et A
et alors tu pourras utiliser la relation indiquée par ton professeur qui est en effet un passage obligé...

Un schéma (considérablement "agrandi" pour être lisible ; l'énoncé dit que les point I, A et J sont très proches les uns des autres, uniquement pour que la valeur de 1 mètre soit valable ; mais tu as déjà utilisé cette donnée).
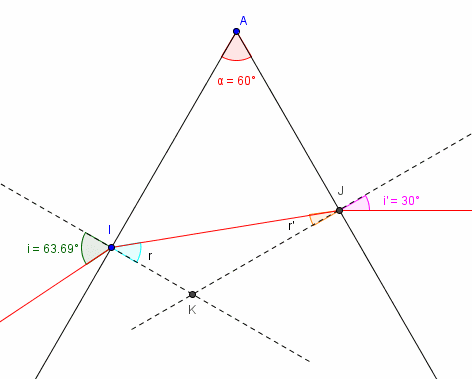
Légende :
A : le sommet du prisme équilatéral où l'angle au sommet vaut  = 60° (on appelle traditionnellement cet angle A ; mais j'ai nommé A le point et Geogebra n'accepterait pas que je donne le même nom à l'angle)
= 60° (on appelle traditionnellement cet angle A ; mais j'ai nommé A le point et Geogebra n'accepterait pas que je donne le même nom à l'angle)
I : le point d'incidence
i  63,69° l'angle d'incidence en I
63,69° l'angle d'incidence en I
r l'angle de réfraction en I
IK : la normale à la face d'entrée en I
J : le point de sortie du rayon
r' : l'angle d'incidence à la sortie du prisme
i' = 30° l'angle de réfraction dans l'air à la sortie du prisme
KJ : la normale à la face de sortie en J
Quelle est donc la relation entre les angles r, r' et  ?
?

Exact.
r + r' = A
et donc...
r' = A - r
et donc...
n.sin(r') = sin(i')
n.sin(A - r) = sin(30°)
n.sin(A - r) = 0,5
Continue !

Même de cette manière j'obtiens des cos et des sin:
N x sin60 x cos r - sin r x cos 60 = 0.5
? Je fais quoi avec cela c'est vraiment mon cul de sac.
Je ne sais pas quoi faire
SVP si vous voyez ce message répondez vite il ne me reste que quelques heures avant la remise de mon défi
Ce n'est pas exactement cela :
n.sin(A - r) = 0,5
d'où
n.[sin(A).cos(r) - sin(r).cos(A)] = 0,5
soit
n.[sin(60°).cos(r) - sin(r).cos(60°)] = 0,5
or
sin(60°) = ( 3)/2
3)/2
cos(60°) = 0,5
et
1.sin(63,69°) = n.sin(r)
encore un petit effort...



