Inscription / Connexion Nouveau Sujet
De la physique dans les Pyramides
Bonjour je dois faire un DM en Physique et malheureusement je bloque.
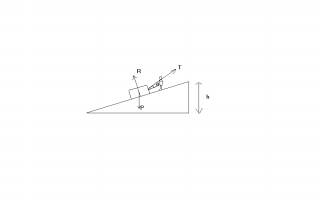
Un homme tire une pierre sur un traîneau par l'intermédiaire d'une corde. La norme maximale de la force T de la traction exercée par l'homme est de 300N. La corde fait toujours un angle  =30° par rapport à la direction de déplacement du traîneau (Cf schéma). La pente du plan incliné est de 6%.
=30° par rapport à la direction de déplacement du traîneau (Cf schéma). La pente du plan incliné est de 6%.
1°) Chercher la signification d'une pente de 6%.
2°) Donner alors la valeur de l'angle  entre le plan incliné et l'horizontale.
entre le plan incliné et l'horizontale.
3°) Faire un bilan des forces s'exerçant sur le système {pierre}.
4°) En négligeant la force de frottement et en considérant que le système garde une vitesse constante vérifier que la masse m peut s'exprimer sous la forme T.cos( ) /g.sin(
) /g.sin( ).
).
5°) Cette fois on ne néglige plus les forces de frottement dont on donne la norme ||f||=k.||Rn|| avec k = 0.242. Exprimer alors la masse m' du système toujours maintenu à une vitesse constante en fonction de k, T, g,  et
et  .
.
6°)Exprimer le travail du poids du système de masse m' entre le bas de la pente et le haut de la pente. Quel est le signe de cette expression ?
7°) Exprimer le travail de la force de traction en fontion de h,T , et
et  .
.
1°) Un pente de 6% signifie qu'à un déplacement horizontal de 10m correspond un déplacement verticale de 6m
2°) sin( )=6/100
)=6/100
 = sin-1 6.00/100=3.43°
= sin-1 6.00/100=3.43°
3°)On a P( le poids), R( la résistance du support) et T (la force de traction).
4°), 5°) et 7°) je n'ai pas réussi
Aider-moi svp
Merci
Bart45
pour la 4, il faut que tu écrives le principe d'inertie et que tu projètes sur l'axe de la pente et sur l'axe perpendiculaire à la pente
c'est ça
en vecteur on écrit : R + P + T = 0
en projection sur un axe parallèle à la pente : - mg.sin alpha + T cos beta = 0
tu comprends ?
J'ai fais la projection mais je ne vois pas le lien entre k, g, b, a, T.
Et je trouve : (m.g)sin  +Tcos
+Tcos +f+Rn = 0
+f+Rn = 0
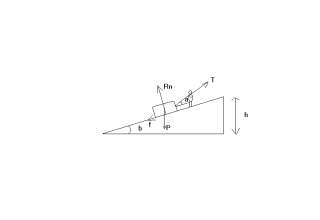
non , en vecteur tu as P + T + Rn + f = 0
en projection sur l'axe de la pente :
-m'g sin  - f + T.cos
- f + T.cos  = 0
= 0
-m'g cos  + Rn + T.sin
+ Rn + T.sin  = 0
= 0
et f=k.Rn
-m'g sin  - k.Rn + T.cos
- k.Rn + T.cos  = 0
= 0
-m'g cos  + Rn + T.sin
+ Rn + T.sin  = 0
= 0
-m'g sin  - k.Rn + T.cos
- k.Rn + T.cos  = 0
= 0
-k.m'g cos  + k.Rn + k.T.sin
+ k.Rn + k.T.sin  = 0
= 0
pour éliminer Rn, on somme les deux équations :
-m'g(sin  + k cos
+ k cos  ) + T.(cos
) + T.(cos  + k.sin
+ k.sin  ) = 0
) = 0
m' = T.(cos  + k.sin
+ k.sin  ) / [ g (sin
) / [ g (sin  + k cos
+ k cos  ) ]
) ]
Mais pour la question 7, comment on peut trouver WabT si on ne peut pas utiliser AB mais les valeurs des angles  et
et  ?
?