Inscription / Connexion Nouveau Sujet
De la lumière dans un prisme
Bonjour, j'ai de gros problèmes avec ce DM qui est a rendre pour lundi 7 janvier. Pouvez vous m'aider ?
Exercice 1. De la lumière dans un prisme [10 pt]
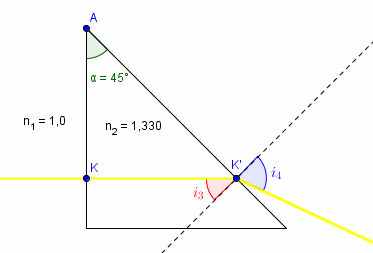
On dispose d'un prisme en verre de cristal, d'indice de réfraction nv = 1,330 et d'angle au sommet  = 45,0°.
On éclaire le prisme par un faisceau de lumière jaune perpendiculairement à la surface de séparation (dioptre air-verre). On
représente ce faisceau par un rayon lumineux qui coupe la surface de séparation air-verre au point K.
1. Préliminaires
a. Comment appelle-t-on le phénomène de déviation de la lumière lors
du passage d'un milieu (milieu 1) 1 à un autre (milieu 2) ?
b. Que vaut la vitesse c de la lumière dans le vide (ou dans l'air) ?
c. L'indice de réfraction se calcule selon la formule n = c/v où v est
la vitesse dans le milieu de propagation et c la vitesse de la question
précédente. Calculer la vitesse de propagation de la lumière dans le
verre en cristal.
Pour les questions suivantes, on rappelle la loi de Descartes : n1
. sin i
1 = n2 . sin i2.
où n1 et n2 sont les indices de réfraction des milieux 1 et 2 ; i
1 et i2 les angles
d'incidence et de réfraction (par rapport à la normale au dioptre).
2. Construction n°1 (au niveau du point K) :
a. que vaut l'angle d'incidence i1 ? Justifier.
b. que vaut l'angle de réfraction i2 ? Justifier.
c. construire, sur le schéma ci-dessus, au niveau du point K, le rayon lumineux à l'intérieur du prisme.
3. Construction n°2 (au niveau du point K') :
Le rayon lumineux à l'intérieur du prisme ressort par le point K'. On appelle i3 l'angle d'incidence avec lequel le rayon lumineux
arrive au point K' et i4 l'angle de réfraction avec lequel le rayon lumineux ressort du prisme.
a. placer le point K' et repérer l'angle i3 sur la figure.
b. montrer que vaut l'angle d'incidence i3 est égal à 45,0°. (utiliser la relation entre les angles du triangle KAK'.)
c. calculer la valeur de l'angle de réfraction i4. Justifier précisément.
d. construire, sur le schéma ci-dessus, au niveau du point K', le rayon lumineux à la sortie du prisme.
4. On remplace le prisme en verre par un prisme de forme identique en glace et on recommence la même expérience. L'angle de
réfraction i4 à la sortie du prisme mesure alors 67,8°.
Déterminer, en justifiant précisément vos calculs, l'indice de réfraction ng du prisme en glace.
Pour la question 1 a) je pense que c'est la dispersion. Pour la b) c'est ~300.000 Km/s pour la c) c'est 300 000/ 206 000 km/s~ 1.45
pour le reste je ne trouve pas merci d'avance pour vos réponses
Bonjour,
Question 1a : non, ce n'est pas cela. Le nom de ce phénomène est un mot qui est employé plusieurs fois dans l'énoncé.
Question 1b : oui, environ 300 000 km.s-1
Très exactement (et par définition) 299 792 458 m.s-1
À noter que le k de km ou de km/s ou de km.s-1... est un k minuscule.
Question 1c : D'où sortent ces valeurs de 206 000 km/s et de 1,45 ? As-tu lu l'énoncé ?

Oui, "réfraction"
Je ne comprends pas cette valeur de la vitesse de la lumière dans le cristal.
Peux-tu vérifier ce que tu as posté. Un indice de réfraction de 1,33 me semble très faible pour du cristal (c'est l'indice de réfraction de l'eau).

Bonjour, j'ai le même Dm qu'eressea, et l'indice de réfraction pour le cristal est bien donné comme étant 1.330, cependant, je trouve que la vitesse de propagation dans le verre en cristal est de 2.25x10^8 m/s.
Ce qui me pose problème, c'est pour justifier les valeur de i1 et i2. Je suppose que i1 est l'angle limite, donc il ferait 48° et i2 =90° (ce qui se confirme dans la question 3b), mais je ne trouve pas la justification adéquate...
Bonjour FelixFelicis
Je suis d'accord avec la vitesse de la lumière dans le cristal que tu as calculée si l'indice de réfraction est vraiment 1,33
Que réponds-tu à la question 2a ?
Rappel :
On éclaire le prisme par un faisceau de lumière jaune perpendiculairement à la surface de séparation (dioptre air-verre).
i1 et i2 les angles d'incidence et de réfraction (par rapport à la normale au dioptre).

J'ai répondu que i1 était égal à 49°, en suivant le calcul que notre prof nous a donné pour calculer l'angle limite en fonction des milieu, ce qui impose i2 à 90°, si je me trompe pas.
donc ça donne
n1siniL = n2sini2
1.33 x siniL = 1
siniL = 1/1.33 = 0.752
sin-1 0.752 = 49

Le faisceau arrive perpendiculairement à la surface de séparation air-verre
Que vaut l'angle d'incidence i1, angle entre le rayon et la normale au dioptre ?

bah 90... je pense que si je me suis trompée c'est que je me figurais un cas de réflexion totale x.x
je suis pas sûre, mais pour i2, c'est tout de même bien égal à 90, non ? puisque l'air est moins réfringent que le cristal, donc il n'y a pas des réflexion, à moins que cette propriété ne s'applique que lors de a réflexion totale ?
Bah... non !

L'angle d'incidence est l'angle entre le rayon et la normale au dioptre.
Si le rayon arrive perpendiculairement au dioptre que vaut donc cet angle d'incidence ?

Que vaut dire "perpendiculairement" ?
Quel est la mesure de l'angle entre une droite et une droite perpendiculaire ?

Une droite est perpendiculaire à une autre droite quand l'angle entre ces deux droite est droit, donc égal à 90, ça, je le sais.
Le faisceau est perpendiculaire au dioptre, donc y a un angle droit, si on ne prend pas en compte la normale. La normale est elle aussi censée être perpendiculaire au dioptre non ?
Très bien !
Le rayon est perpendiculaire au dioptre, donc fait un angle de 90° avec le plan du dioptre
La normale à un plan fait elle aussi un angle droit, de 90°, avec toutes les droites du plan
Quel est donc l'angle entre le rayon et la normale (c'est cet angle que l'on nomme "angle d'incidence") ?

Mais bien sûr !
Puisque le rayon arrive perpendiculairement au dioptre, l'angle d'incidence est nul.
Donc i1 = 0°
Je suppose que tu peux en déduire immédiatement la valeur de l'angle de réfraction i2.
La construction ne devrait donc pas poser de difficulté.

Oui, merci beaucoup pour votre aide. J'aurais sans doute compris plus vite si on avait vu cette propriété en cours x.x
0 aussi je pense, mais comme le faisceau est perpendiculaire, il pourrait tout aussi bien faire 90°. Mais je penche plus pour 0 =)
Il NE peut PAS valoir 90°.
L'angle de réfraction est l'angle entre le rayon réfracté et la normale au dioptre (comme l'angle d'incidence est l'angle entre le rayon incident et la normale au dioptre).
Un rayon qui arrive sur un dioptre perpendiculairement à la surface de ce dioptre n'est pas dévié.
Si les "formules" te rassurent :
n1.sin(i1) = n2.sin(i2)
Pour le rayon incident :
n1 = 1
i1 = 0°
Pour le rayon réfracté :
n2 = 1,33
donc sin(i2) = 0
et la solution est i2 = 0°