Inscription / Connexion Nouveau Sujet
Compréhension puissance réactive
Bonjour,
En cherchant un peu tout seul a essayer de comprendre qu'est ce que la puissance réactive, je me heurte à un petit exercice que je ne comprend pas.
L'énoncé est le suivant:
Une lampe fluorescente est alimentée sous 230 volts alternatif. Un courant total de 0,5 ampère est mesuré. La lampe comporte un récepteur résistif, le tube lumineux, et un récepteur inductif, le ballast.
Le courant total sera déphasé de phi = 60°. Il est constitué par la somme de la composante en phase avec la tension pour le tube (Iw) et de la composante déphasée de 90° pour le ballast (Ib).
Si un condensateur est placé en parallèle sur l'installation, et qu'il est dimensionné de telle sorte qu'il appelle un courant exactement égal à celui du ballast, calculez la puissance Active et réactive.
De ce que je comprend :
1) Le courant capacitif est en opposition de phase par rapport au courant inductif (le courant capacitif est 90° en avance et le courant inductif est 90° en retard sur la tension) -> leur somme est nulle.
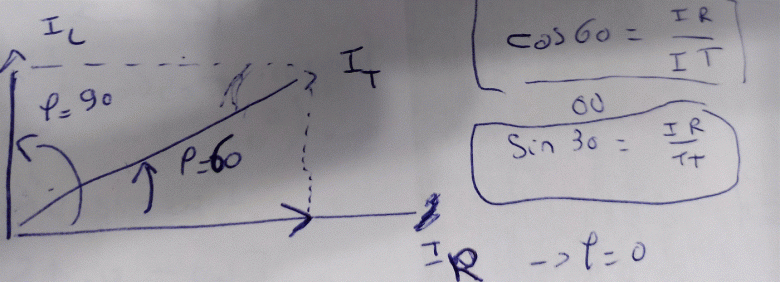
2)Le courant total est équivalent au courant résistif dans le tube. Pour chercher ce courant je dois donc decomposer comme dans l'image.
je trouve donc 0.25.
Quelque chose m'échappe, quand j'essaie de calculer I de l'impédance avec la même méthode je ne trouve pas 0.25.
Du coup je me demande si c'est pas un coup de chance ma règle trigo ?
Ils ont la même pulsation pourtant.
En vous remerciant,
Bonsoir
Le courant résistif à bien pour intensité efficace 0,25A (ne pas oublier l'unité).
Quelque chose m'échappe, quand j'essaie de calculer I de l'impédance avec la même méthode je ne trouve pas 0.25.
Pour obtenir cette valeur par la relation I=U/Z tu dois choisir l'expression de l'impédance prenant en compte le condensateur.Si tu ne prends en compte que la résistance et l'inductance, tu vas obtenir 0,50A...
Bonsoir,
Merci pour votre réponse.
Pk si je prend sin phi = I bobine / I tot
donc I bobine = Itot * sin phi et le résultat est différent de 0.25.
Or dans ma tête itot = i bobine + i r
ir = 0.25 et itot = 0.5. Donc je m'attendez a trouver 0.5
C'est cela que je comprend pas.
Attention : la relation que tu écris entre les intensités s'applique aux valeurs instantanées et aux vecteurs de Fresnel associés mais pas aux valeurs efficaces sauf cas très particuliers.
D'accord,
Du coup c'est un cas particulier le premier calcul de Ir ?
Ce que j'aimerai comprendre c'est justement pk la lecture sur l'axe des abscisses est bonne et pas l'axe des y 
Il y a t'il une autre méthode que la trigo ?
OU c'est la bonne méthode que j'utilise ?
J'aimerai comprendre ce qu'il ne faut pas faire, pour pas me tromper dans un autre exercice 
Car la j'ai le sentiment d'avoir eu de la chance
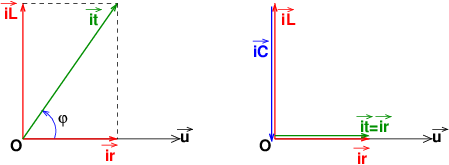
Premier cas : ballast en parallèle avec lampe soit R en parallèle avec L : en valeurs instantanées :
it=ir+iL d'où les vecteurs de Fresnel de la figure de fauche, ceux que tu as représentés ; les valeurs efficaces :
Ir=It.cos( ) ; IL=It.sin(
) ; IL=It.sin( )
)
Deuxième cas : on ajoute un condensateur en parallèle (R//L//C) donc en valeurs instantanées (figure de droite):
it=ir+iL+iC avec en plus : iL+iC=0 ; donc :
it=ir
En valeurs efficaces :
It=Ir.
Merci beaucoup c'est bcp plus claire que moi 
Je suis tout a fait d'accord avec vous, mais si je fais;
Dans le premier cas,
IL= It.sin(phi) = 0.5 * sin(60) = 0.43A
ir = It.cos(phi) = 0.5 * cos(60) = 0.25A
or it=ir+iL et it = 0.5 A
donc 0.5 = 0.43+0.25 ce n'est pas vrai. C'est ca que je ne comprend pas 
Je suis désolé mais çà m'échappe! j'aimerai comprendre ^^
Je te l'ai déjà dit mais je vais me répéter :
la relation que tu écris entre les intensités s'applique aux valeurs instantanées et aux vecteurs de Fresnel associés mais pas aux valeurs efficaces sauf cas très particuliers.
D'accord, du coup le bon raisonnement est le suivant:
1) je calcul par trigo Ir = 0.25A.
Et après je calcul la puissance active et réactive associées
En vous remericant
Attention : une fois placé le condensateur, les valeurs de Ir et It ne sont pas nécessairement égales à celles obtenues en absence du condensateur.
En présence du condensateur, la valeur de la puissance réactive s'obtient sans calcul.
Dans ton raisonnement, pense à bien préciser s'il correspond ou non à la présence du condensateur.


