Bonjour,

Pour le calcul de l'angle, vous parlez de l'angle A différent de .
J'ai du mal à voir cet angle A et votre triangle rectangle d'hypothénuse 99,6.
Un dessin montrant le dit triangle et l'angle A, peut-être ?
Quatre chiffres significatifs me paraissent un peu trop.

Sinon on a bien besoin de pour les calculs et c'est mesurable avec un rapporteur.

Vous n'avez pas à calculer la résultante : elle est donnée 150 N.
Par contre, il vous faut la projeter sur les axes x et y, d'où la nécessité de l'angle .
Vous savez projeter un vecteur ?
Idem pour , mais là c'est plus immédiat, il faut simplement traduire le dessin.

J'ai modélisé le triangle donc je parlais comme ceci :

Bonjour,

J'ai compris pour l'angle A et AB=99,6mm, c'est exact. Mais cela n'est pas très utile : la question est de trouver les composantes de . Sur le dessin que vous avez fait, les composantes en x et y sont représentées par quelles longueurs ?

Une remarque : éviter de noter avec le même nom deux points différents (B et B sont différents, comme C et C).

J'ai pensé à utiliser le cos avec la force de F mais nous n'avons aucune longueur sur le triangle rectangle que je vous ai dessiné en dessous donc je ne comprends pas.
Nous avons fais un exercice du même type où l'on devait calculer des composantes mais je n'avais pas du tout compris donc voilà...

oui il faut une autre valeur pour calculer le cos non ?

je prends 90° ?

L'angle , vous le mesurez au rapporteur.

Sur la feuille, c'est écrit que ce n'est pas les vrais dimensions et notre professeur ne nous as jamais dit de mesurer l'angle, de plus l'exercice n'est pas imprimé et n'ayant pas d'imprimante, je ne peux pas mesurer l'angle...

Comment avez-vous mesuré alors le 99,6 mm ?

Si vous avez réussi à déterminer A, faites de même avec le triangle AB'C' (celui de la force) pour trouver

Nous avons calculer le 99,6 mm  en utilisant le théorème de pythagore en nous servant des mesures 23mm et 97mm Donc cela nous a fait hypothénuse = 97²+23² et la racine carré donne 99.6mm.
Pour ce qui est de A (dans le triangle AB'C') c'est que je ne sais pas si nous pouvons dire que le côté adjacent à A est aussi égal à 150 N ou non... Cela faciliterait les choses. Et je me demande aussi si l'angle en A (dans le triangle de la force) est aussi égal à 13.12° comme je l'avais calculé pour l'autre triangle (celui sur la clé) .

Le seules mesures donc vous avez besoin pour sont les 23 et 97 mm.

L'angle A n'a aucune raison d'être égal à , sauf par hasard.

Pour la force,  il faut considérer que votre triangle AB'C' est dessiné à une échelle telle que AC'=150 N, vous pourrait alors en déduire AB' et B'C'. Si vous n'avez aucun moyen de mesurer, alors je ne sais pas.
Solution 1 : poser votre rapporteur sur l'écran
Solution 2 : poser le double décimètre sur l'écran et mesurer AB' B'C' et AC'.
Solution 3 : trouver un logiciel capable de faire des mesures sur une image, vous avez cela dans vos outils

Je vais essayer...

Le mieux serait quand même que soit fourni, il n'est pas caché quelque part dans les question suivantes ou autre.

Non j'ai vérifié mais il n'est pas donné 😕

Dernière possibilité : on vous demande un calcul littéral (avec donc) et à la fin, il y a une question du type "déterminer pour que le moment soit maximal."

Malheureusement la deuxième question est la suivante : "Calculer les moments des composantes en Fx et Fy en B, sans oublier de dessiner leur bras de levier pour en déduire :  

Je ne vois pas trop l'intérêt de calculer séparément les moments des composantes, chaque calcul étant aussi compliqué que le calcul direct du moment de la force.

Commençons donc par la fin : que savez-vous du moment d'une force en un point ?

J'ai enfin compris !

Je suppose que vous avez défini le moment comme force x bras de levier.

Si vous prenez Fx, quel est le bras de levier ?
Si vous prenez Fy, quel est le bras de levier ?

Je ne comprends pas...

Est-ce que vous avez défini le moment par force x bras de levier ?
Sinon, comment l'avez-vous défini ?

Non je n'ai pas défini le moment par force x

OK, et donc comment l'avez-vous défini ?

sur x cest distance  x Fx et Fx= F x cos(alpha)

Je pensais à quelle chose du genre : .
Cela vous dit quelque chose ?

Je vois à peu près (nous n'avons pas eu beaucoup de cours sur cette partie) donc si je comprends bien, je dois écrire M(F) = 150* OH (OH étant inconnue sauf si l'on prend une valeur dans l'exercice et la convertir en mètres...)

Ou bien ducoup si nous prenons une valeur dans l'énoncé, je prendrais le 97mm donc cela fait 0,097, que nous remplaçons par OH Donc :
M(F) = 150 * 0,097 = 14,55 N/m ?

Peut-on utiliser :
Fx - 150cos(alpha) = 0  ->   Fx = 150sin(alpha)     (composante de Fx)  ?
Fy - 150sin(alpha)  = 0  ->   Fy = 150cos(alpha)    (composante de Fy)  ?

Oui c'est bien cela à quelques bémols près :
- je ne vois pas d'où sort cette somme égale à 0
- le implique passe d'un cos à un sin
- le point de départ est la projection, donc la deuxième partie (après le -> )
- alpha est a priori non orienté (double flèche), donc il faut regarder le dessin et sur celui-ci on voit que Fx et Fy sont négatifs, donc

Fx = -150 sin(alpha)  
Fy = -150 cos(alpha)  

Donc si je comprends bien pour calculer M(Fz) nous faisons:
97 * (-150)sin(alpha) + 23*(-150)cos(alpha) ?

Dernier petit problème, dans la formule permettant de calculer un moment OH étant inconnue, puis-je mettre une autre distance, comme 97 dans ce cas ?

Je mets un dessin pour mieux voir :

Quel est le bras de levier (votre OH) de Fx ?
dito Fy ?

Dans quel sens Fx fait-il tourner la clef ?
dito Fy ?

Le bras de levier de Fx est AB et celui de Fy est AC' (c'est ce que j'essaye de m'imaginer) ?

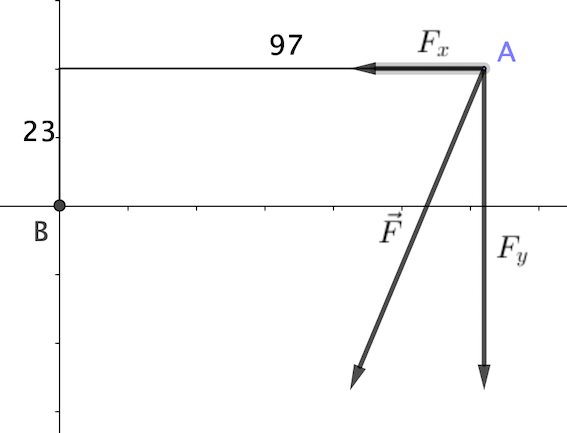
Le sens de Fx est de A vers B et le sens de Fy est de A vers B' (selon le schéma avec les points que j'ai réalisé plus haut)

"On appelle «bras de levier» d'une force F⃗ par rapport à un axe de rotation ∆ la distance entre la ligne d'action de F⃗ et l'axe de rotation.
C'est la longueur du segment qui lie l'axe ∆ à la ligne d'action de la force, le segment étant perpendiculaire à cette ligne d'action."

Ici l'axe est en B.  AB n'est perpendiculaire ni à F ni à Fx ni à Fy
La "ligne d'action" de Fx est horizontale, donc la distance doit être prise verticalement soit 23.
La "ligne d'action" de Fy est verticale, donc la distance doit être prise horizontalement soit 97.

Voir les schémas ci-dessous.

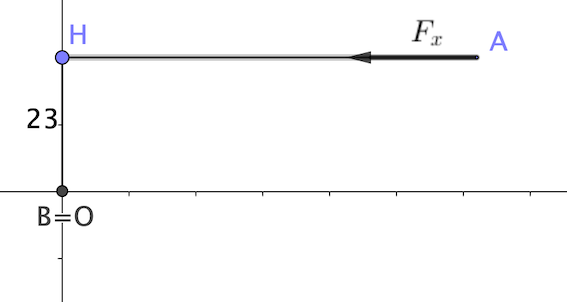
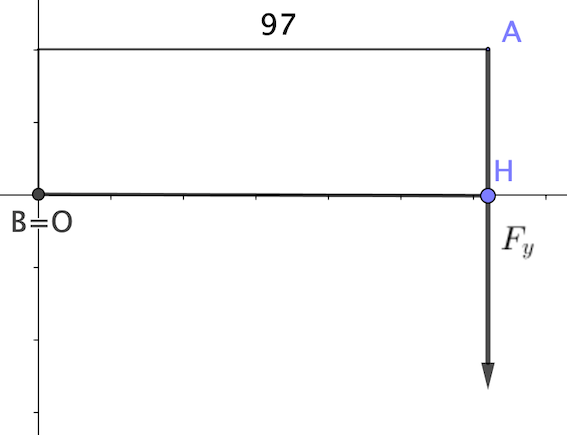
Oohh je viens de comprendre merci beaucoup 😉 (je comprends beaucoup mieux avec des schémas). Donc si je résume, le OH en question de Fx doit être pris verticalement et le OH de Fy doit être pris horizontalement ce qui nous donne
M(Fx) = -150sin(alpha) * 23
M(Fy) = -150cos(alpha) * 97 ?

C'est bien cela, il reste les problèmes de signe : le signe concerne le sens dans lequel on tend à faire tourner la clef, c'est un sens de rotation, pas l'orientation de F.

Le signe est lisible sur la figure ou pas ?.

Oui

Si on tend à lever la clé en angle droit, le signe sera positif ?

Si on "lève" la clef (du côté A), oui la valeur sera positive (on tend à tourner dans le sens x -> y qui est le sens positif.

Donc le signe change M(Fz) ?

Je n'ai pas bien compris ce que le signe représentait ici...

F_x fait tourner dans le sens x->y (inverse aiguille d'une montre), doit donc être compté positif,
F_y fait tourner dans le sens y->x (sens aiguille d'une montre), doit donc être compté négatif,

Soit M= + abs(F_x).23  - abs(F_y).97 en N.mm

Ah d'accord je viens de comprendre !
Mais que représente les "abs" ?

abs(x) pour valeur absolue de x

Ah d'accord ! merci beaucoup pour votre aide et votre temps que vous avez mis pour m'aider (je suis un peu long à la détente 😅). Je vais faire le reste de mes exercices tout seul avec ce que vous m'avez appris !