Inscription / Connexion Nouveau Sujet
Chariot qui monte
Bonsoir, j'ai besoin d'aide sur un exercice, merci.
1°) Rempli de matériaux, un chariot est tiré par une corde et monte à vitesse constance le long du plan incliné. La masse du chariot et de so chargement est M=480kg. Pour simplifier l'étude, on néglige tout frottement. On représente la réaction du plan incliné sur les roues du chariot par une force unique vecteur R appliqué en B. La direction de cette force est normale au plan incliné.
a) Définir le système étudié et le référentiel utilisé. Système : Chariot, référentiel : Terrestre
b) Quelles sont les forces agissant sur le système ? P, R et T
c) Quelle relation vérifient les vecteurs force en puissance en présence ? P + R + T = 0
2°) Par une méthode graphique, déterminer la valeur T de la tension de la corde et la valeur R de la réaction du plan incliné.
On utilisera l'échelle : 100mm 1000N ( Je trouve R = 3600N, T = 2900N et P = 4700N )
3°) Déterminer les valeurs T et R au moyen de projections sur deux axes orthogonaux convenablement choisis Je ne comprends pas la question.
Les première questions j'y arrive, mais pour les deux dernières je n'en suis pas sûr. ( J'arrive pas la dernière )
De plus je crois qu'ils se sont trompés pour l'échelle
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
Bonjour,
1. a.
* système : le chariot de masse M et de centre d'inertie G
* référentiel : le sol, terrestre supposé galiléen
b. Bilan des forces :
* le poids du chariot
* la réaction du support
* la tension exercée par la corde sur le chariot :
c. Le chariot monte à vitesse constante, donc d'après la première loi de Newton :
2. Il faut expliquer tes calculs !
* P = M.g = 480.9,8 = 4700 N
* R est à déterminer sur le schéma :
sa norme vaut R = .... cm donc avec l'échelle R = .... N
* Avec la relation précédente :
<=>
Par la relation de Chasles ou la règle du parallèlogramme on détermine graphiquement T = ...... cm = ..... N
3. Choisissons la base qu'on place sur le schéma :
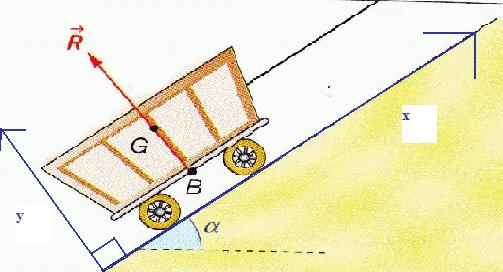
On lit et on exprime les composantes de chaque force en fonction de :
La réaction :
/x : 0
/y : + R
Le poids :
/x : P.cos(90 + )
/y : -P.cos()
La tension :
/x : +T
/y : 0
On repart de la relation
/x : P.cos(90+) + 0 + T = 0
soit T = ......
/y : -P.cos() + R + 0 = 0
soit R = ........
Calculs à vérifier 
Ok, mais à vrai dire, je vais vous dire la vérité : Je ne comprends rien pour P ! C'est à dire, j'arrive pas à savoir où est P sur cet axe ( J'ai une idée, mais j'en suis pas sûr). Je ne sais pas quand est-ce qu'il faut utiliser cos ou sin, pourriez-vous m'éclaircir s'il vous plaît ?
Oui ça j'ai compris, mais il peut être "déplacer" sur l'axe (x;y) non ?
Ca nous donnerais donc Le poids :
/x : -P.sin(alpha)
/y : -P.cos(alpha)
Non ?


