Niveau seconde

champ magnétique

Posté par
handa 31-03-20 à 04:45

Bonjour, j'ai un exercice de physique sur le champ magnétique
L'énoncé est le suivant :
je sais pas comment faire à résoudre la question 2
merci de m'aider
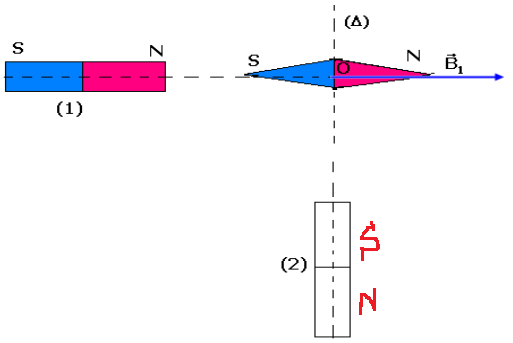
On place une aiguille aimantée en un point O de l'axe d'un aimant droit (1). On observe alors que cette aiguille s'oriente suivant l'axe du vecteur B₁. B₁=5mT
Lorsqu'on place un deuxième aimant droit (2), l'aiguille dévie d'un angle $\theta =25°$ dans le sens de rotation des aiguilles d'une montre.
1/  déterminer les caractéristiques du vecteur B₂ crée par (2) au point O et montrer sa polarité.
2/ De quel angle   $\alpha$   faut-il faire tourner l'aimant (2) (dans le plan constitué par les deux axes des aimants), et par suite son axe, autour de O pour que la déviation de l'aiguille serait $\theta '=20°$ . Montrer le sens de cette rotation.
on néglige le champ magnétique terrestre.

Mes réponses:
1/ Origine : le point O
     Sens : du bas vers le haut (déviation de l'aiguille dans le sens de rotation des aiguilles d'une montre)
     Direction: perpendiculaire à B₁
     Intensité :  tan $\theta$ = $\frac{B2}{B1}$
         Donc  :     B₂=2,33mT

merci d'avance

champ magnétique

Posté par re : champ magnétique 31-03-20 à 18:55

Bonjour,
Question 1 :
OK pour B₂= 2,33 mT

Question 2 :
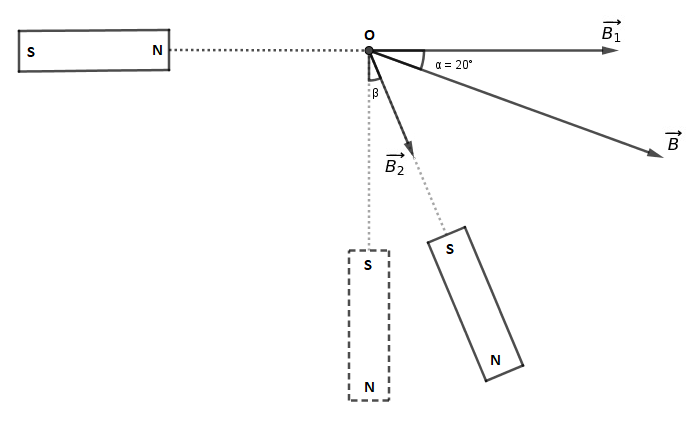
Ci dessous, ce que je crois avoir compris de l'énoncé.
Je pense qu'on demande de calculer la valeur de l'angle en conservant B₁ = 5mT et B₂ = 2,33 mT

champ magnétique

Posté par re : champ magnétique 01-04-20 à 01:21

Merci  beaucoup  odbugt1
j'ai fait  le même dessin, mais je me bloque dans les calculs soit par:
*Application du théorème d'alkaschi
* Soit par projection sur un repère (O,x,y)
   $\vec{B}=\vec{B1}+\vec{B2}$
sur Ox:   $Bcos\theta '=B1+b2.sin\alpha$
sur Oy:   $-B.sin\theta '=-B2.cos\alpha$
   tan $\theta '$

je trouve toujours une équation à plusieurs inconnus
merci de m'aider

Posté par re : champ magnétique 01-04-20 à 10:22

Utilise le théorème des sinus pour calculer l'angle entre $\overrightarrow{B}$ et $\overrightarrow{B_2}$
Tu obtiendras ensuite l'angle par simple différence.

Posté par re : champ magnétique 03-04-20 à 04:27

Merci odbugt1  pour votre aide.
J'ai fait deux méthodes qui donnent deux valeurs différentes
Méthode1 : Lois des sinus
$\frac{sin\beta }{B1}=\frac{sin\theta '}{B2}$
Cela conduit à : $\alpha =23°$
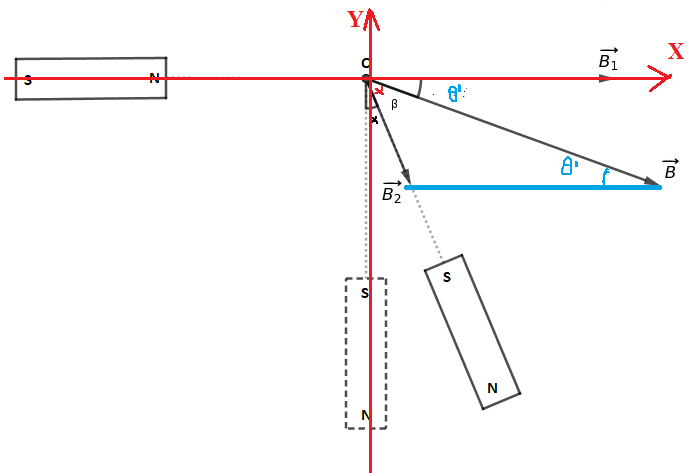
Méthode2
Soit par projection sur un repère (O,x,y) de :   $\vec{B}=\vec{B1}+\vec{B2}$
         * Sur OX:     $B.cos\theta '=B1+B2.sin\alpha$
         * Sur Oy:     $-B.sin\theta '=-B2.cos\alpha$
  donc : $tan\theta '=\frac{B2.cos\alpha }{B1+B2.sin\alpha }$
On pose : t= $tang\frac{\alpha }{2} \\ c'est-à-dire que : sin\alpha =\frac{2t}{1+t²} et cos\alpha =\frac{1-t²}{1+t²}$
On trouve l'équation suivante :
$(B1.tang\theta '+B2)t²+2.B2.tan\theta '+(B1.tan\theta '-B2)=0$
La résolution de cette équation conduit à choisir la solution positive: t=0,1
donc:   $\alpha =11,5°$

champ magnétique

Posté par re : champ magnétique 03-04-20 à 12:31

Tu sembles avoir oublié le " t " de ton équation :

$(B1.tang\theta '+B2)t²+(2.B2.tan\theta ')t+(B1.tan\theta '-B2)=0$

J'ai obtenu :
4,1514 t² +1,6972 t - 0,5117 = 0
qui donne t=0,2018 et au final le même résultat que par la loi des sinus.

Posté par re : champ magnétique 05-04-20 à 01:18

Exactement Mr. odbugt1
Merci beaucoup
J'ai une dernière question : avec quel outil vous avez dessiner la figure ci-dessus.
Merci d'avance

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau seconde
49 fiches de physique - chimie en seconde disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

champ magnétique

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique