Inscription / Connexion Nouveau Sujet
Champ magnétique 3
Bonjour à tous ;
J'ai un petit exercice merci beaucoup d'avance !
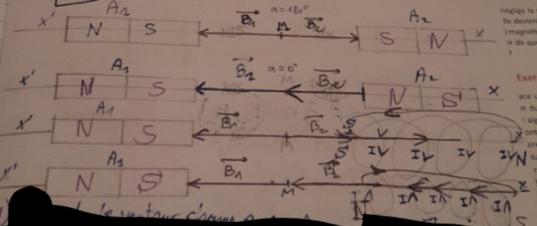
La figure ci-dessous montre deux aimants droits A1 et A2 sont placés sur l'axe x'x
Chacun d'eux crée au point M situé à égale distance des deux sources, un champ magnétique de 20 mT.
Voici le schéma ;
1) Représenter le vecteur champ magnétique en M, lorsque les deux pôles en regard sont de même nom.
2) Même question lorsque les deux pôles sont de noms différents.
3)On remplace l'aimant A2 par un solénoïde S2.
On désire qu'au point M le champ résultant ait une norme égale à 60 mT.
4)Quelle doit être la norme du champ magnétique créé par le solénoïde ? (Deux cas sont envisageables).
5) Pour chaque cas, quel est le sens du courant dans le solénoïde ?
J'ai pas compris la 4 et 5
Une petite indication s'il vous plaît et merci beaucoup d'avance !
Bonjour,
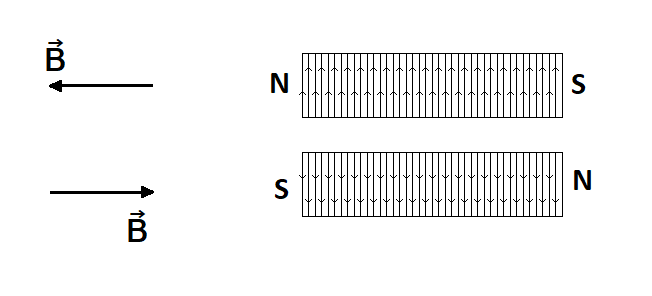
Le solénoïde, s'il est parcouru par un courant, se comporte comme un aimant droit.
La nature des pôles de l'aimant (N et S) dépendent du sens du courant.
Bonjour ;
Merci beaucoup de m'avoir répondu !
Est ce que on a les même vecteur champ magnétique même si on a remplacé le vecteur par un Solénoïde?
Je ne comprends pas comment on peut remplacer un vecteur (qui est un objet mathématique) par un solénoïde (qui est un objet matériel).
Je répète :
Le solénoïde, s'il est parcouru par un courant, se comporte comme un aimant droit.
Le solénoïde, s'il est parcouru par un courant, se comporte comme un aimant droit.
Ça vous dire que le solénoïde aussi contient pôle Nord et Sud (sachant que nous laissons les pôles Nord et Sud comme avant )
Oui,
On parle plutôt dans le cas d'un solénoïde de faces Nord et Sud
Tout se passe comme si tu remplaçais l'aimant A2 par un autre aimant créant au point A un champ magnétique dont il faut trouver la valeur.
Donc on a la même chose que les deux premières ?
Pour l'intensité du champ créé par un solénoïde on a le champ résultants
B =60mT et l'intensité du champ magnétique de l'aimant A1 est B1=20mT
L'intensité de solénoïde est B2
On a aucune information sur la longueur et nombre des spires
Donc est ce que on peut utiliser la relation
B2=B12+B22+2B1B2cos(;
?
Pour le schéma, c'est bon.
Si on inverse le sens du courant les polarités N et S sont inversées et le sens du champ magnétique également.
Les champs ont tous les trois la même direction.
Il en résulte que suivant les cas B est égal soit à la somme, soit à la différence des champs B1 et B2
L'énoncé donne B = 60mT et B1=20mT
Il est donc très simple de trouver la valeur du champ B2 créé par le solénoïde ( il existe 2 solutions qui diffèrent en fonction du sens du courant)
Tu n'as pas besoin de connaître la longueur du solénoïde et le nombre de spires.
Bonsoir,
Merci beaucoup de m'avoir répondu ;
=
Donc
B2=B12+B22+2B1B2cos(;
(Avec  =180°)
=180°)
Ou
Donc
B2=B12+B22-2B1B2cos(;
(Avec  =0°)
=0°)
C'est bon, mais il est un peu ridicule d'utiliser le théorème d'Al-kashi pour le cas simplissime de vecteurs ayant la même direction.
Bonsoir ;
Merci beaucoup de m'avoir répondu !
1 ère relation
J'ai trouvé B2=142,46mT
2 ème relation
J'ai trouvé B2=40mT.
Lorsque les champs et
sont de même sens :
B = B1 + B2
B2 = B - B1 = 60 - 20 = 40mT
C'est ce que tu as trouvé.
Lorsque les champs et
sont de sens contraires :
B = B2 - B1
B2 = B + B1 = 60 + 20 = 80mT
Désolé erreur de ma part
(
 =180°)
=180°)
1 ère relation
J'ai trouvé B2=142,46mT=80mT
(
 =0°)
=0°)
1er relation
J'ai trouvé B2=40mT
2ème relation j'ai trouvé B2=80mT
Merci beaucoup à vous !
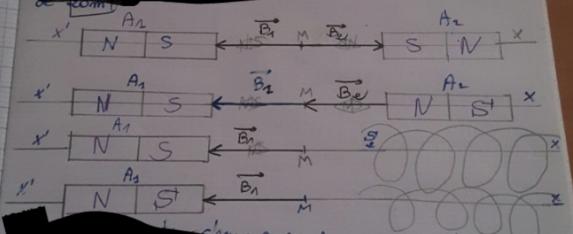
Bonsoir à tous;

Est ce que c'est correct ?(pour le sens de courant électrique et les autres)
Merci beaucoup à vous !
Bonsoir ;
Donc mon figure est correct ?
Désolé erreur de ma part
(
 =180°)
=180°)
1 ère relation
J'ai trouvé B2=142,46mT=80mT
(
 =0°)
=0°)
1er relation
J'ai trouvé B2=40mT
2ème relation j'ai trouvé B2=80mT
Merci beaucoup à vous !
Est ce que ça est correct ?
Merci beaucoup à vous !
Pour l'intensité on a deux cas
B2=80mT ou B2=40mT
Oui, tu avais déjà obtenu ce résultat le 30-03-20 à 20:21