Inscription / Connexion Nouveau Sujet
Centre de gravité
Bonjour j'ai besoin d'aide pour me corriger s'il vous plaît car je suis pas sure de ma réponse.
Voici l'énoncé :
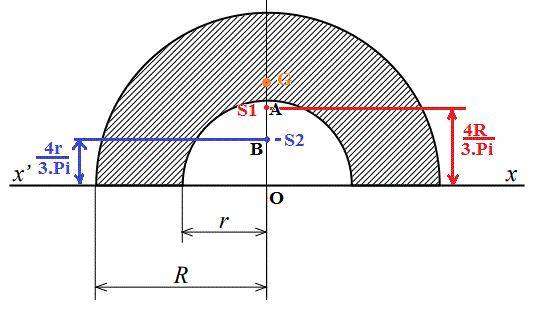
Trouver le centre de gravité de la figure ci-dessous et les valeurs de son moment statique par rapport à l'axe x'x.
Tout d'abord les formules générale puis faire l'application
Application : R = 15 cm ; r = 5cm.
Voici mon raisonnement
d est la distance du centre de gravité.
La application du théorème de GULDIN me dit =
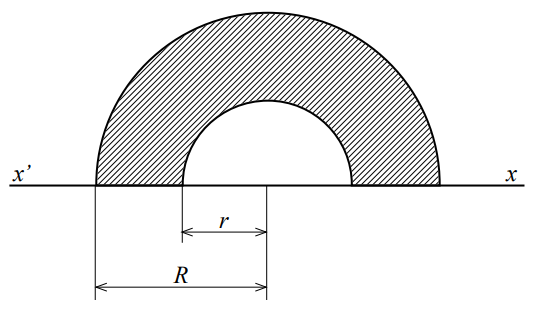
On demande d'abord la formule générale, c'est-à-dire la formule littérale donnant la distance d du centre de gravité de la demi-rondelle au centre des demi-cercles en fonction des rayons r et R de ceux-ci. L'as-tu établie ?
J'ai calculer la surface totale des demi-cercles ensuite, j'ai utiliser le théorème de GULDIN pour le moment statique.
Pour la distance d du centre de gravité je les calculée par la formule ;
Ms = S x d
Et vous me demande quoi la formule littérale c'est-à-dire ?
Il s'agit d'exprimer la longueur d en fonctions des rayons R et r .
Ensuite, pour l'application numérique relative au présent problème, il suffit de remplacer, dans l'expression trouvée, R et r par leurs valeurs numériques.
Mais l'énoncé dit bien " Trouver le centre de gravité de la figure ci-dessous ".
Où l'as-tu trouvé, ce centre de gravité ?
Bah non ! Tout d'abord il faudra calculer le moment statique de chaque demi-cercle de la formule suivant :
Tout d'abord il faudra calculer le moment statique de chaque demi-cercle de la formule suivant :
C'est bien sa ?
Pourtant, dans l'énoncé, la position du centre de gravité est citée avant la valeur du moment statique.
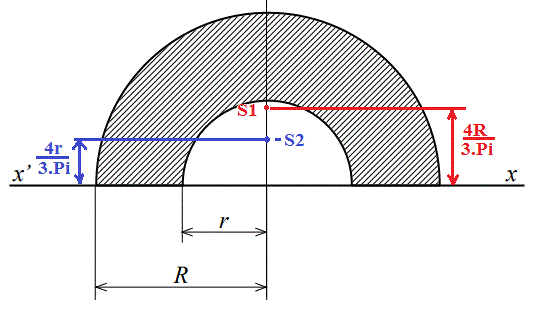
C'est OK avec d = 4r/(3Pi) ... pour un demi disque plein.
Cela signifie que le centre de gravité d'un demi disque (complet) de rayon R est à la distance 4R/(3Pi) de l'axe X'X
Cela signifie aussi que le centre de gravité d'un demi disque (complet) de rayon r est à la distance 4r/(3Pi) de l'axe X'X
Or l'aire du demi disque de rayon R est S1 = Pi.R²/2
et l'aire du demi disque de rayon r est S2 = Pi.r²/2
On pourra déterminer le centre de gravité de l'aire hachurée en cherchant celui de 2 "masses".
Une "masse" ayant la mesure de S1 située à la distance 4R/(3Pi) de l'axe X'X
Et l'autre "masse" ayant la mesure de - S2 située à la distance 4R/(3Pi) de l'axe X'X
ATTENTION : l'aire S2 est prise en négatif dans le calcul du G global car c'est l'aire MANQUANTE du disque de rayon R pour trouver la partie hachurée.
Voila, il n'y a plus qu'à ...
Sauf distraction. 
Bonjour, J-P
Je te remercie pour tous ces renseignements je pense que j'ai compris.
Voici mon raisonnement Peux-tu me confirmer cela ?
Après je doit appliquer la formule :
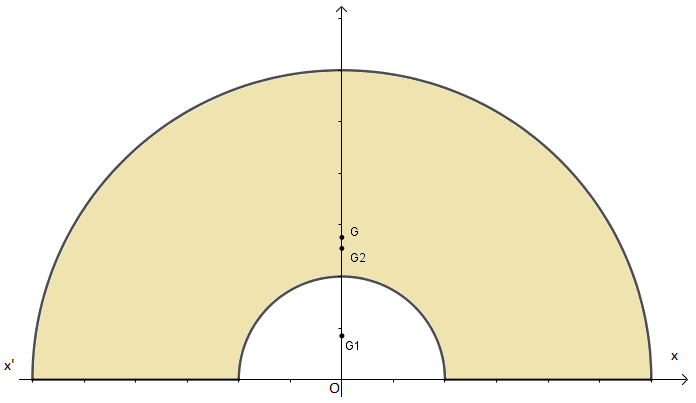
Le calcul du moment statique par rapport à l'axe x'Ox nécessite de connaître la distance OG entre cet axe et le centre de gravité G de la surface colorée.
Observe la figure jointe : G1 est le centre de gravité de la partie manquante, G2 le centre de gravité du demi-disque plein et G le centre de gravité de la partie colorée.
Tant que tu n'auras pas suivi les conseils de JP et trouvé cette distance OG ( qui n'est pas comme tu sembles le croire égale à OG2-OG1) tu ne pourras pas calculer le moment statique.
Et puis, fais un peu attention aux unités : Une aire en cm, une longueur en cm3 cela ne fait pas très sérieux !
Ton calcul de OG est faux.
JP a expliqué :
On pourra déterminer le centre de gravité de l'aire hachurée en cherchant celui de 2 "masses".
Une "masse" ayant la mesure de S1 située à la distance 4R/(3Pi) de l'axe X'X
Et l'autre "masse" ayant la mesure de - (S2) située à la distance 4r/(3Pi) de l'axe X'X
ATTENTION : l'aire S2 est prise en négatif dans le calcul du G global car c'est l'aire MANQUANTE du disque de rayon R pour trouver la partie hachurée.
J'ai seulement corrigé (en rouge) une faute de frappe.
Trouver la position de G revient à trouver le centre de gravité du point G2 affecté de l'aire S2 et du point G1 affecté de l'aire (-S1)
Je suis vraiment désolé mais je vous suis pas... J'ai passée une journée à assez chargée au boulot et avec la chaleur c'est pas gagnée.
Bon je vais faire tout les calculs qu'on a besoin.
Apres cela, je doit faire une soustraction de -S1 sur G1 mais comment ??
Tes résultats sont justes.
Mais, pour calculer OG, il faudrait que tu écrives d'abord la relation qui lie S1, S2, OG1, OG2 et OG.
Bon, faisons le point.
Depuis le début tu calcules les valeurs numériques de S1, S2, OG1, OG2 et tu finis par obtenir les bons résultats avec l'unité adéquate, sans te rendre compte que ce n'est pas ce qu'on te demande.
En revanche tu ne tiens aucun compte de
a) L'énoncé qui stipule clairement :
Tout d'abord les formules générales puis faire l'application
b) Des conseils de Priam qui te rappelle et précise les exigences de l'énoncé :
Il s'agit d'exprimer la longueur OG en fonction des rayons R et r .
c) De la méthode indiquée par JP (avec schéma à l'appui)
On pourra déterminer le centre de gravité de l'aire hachurée en cherchant celui de 2 "masses".
Une "masse" ayant la mesure de S1 située à la distance 4R/(3Pi) de l'axe X'X
Et l'autre "masse" ayant la mesure de - S2 située à la distance 4r/(3Pi) de l'axe X'X
d) De mes propres indications :
Trouver la position de G revient à trouver le centre de gravité du point G2 affecté de l'aire S2 et du point G1 affecté de l'aire (-S1)
Petite question susceptible de t'aider :
Sais tu trouver la position du centre de gravité de deux points matériels A et B dont les positions et les masses sont connues ?
Si deux points A et B ont pour masses respectives a et b , et si G est leur centre de gravité, M étant un point quelconque, on a la relation vectorielle
aMA + bMB = (a + b)MG .
Ici, on pourra choisir comme point M le point O et, comme "masses", les aires des pièces semi-circulaires considérées.
Avec les indications données par Priam tu devrais maintenant trouver la relation entre
puis écrire cette même relation mais cette fois ci entre
Bonjour merci pour la relation mais dans mes cours je ne la trouve pas...J'ai trouve cela sur internet

Dans le présent exercice, il s'agit de déterminer le centre de gravité G1 du grand demi-disque en considérant ce dernier comme la réunion d'un petit demi-disque matériel de centre de gravité G2 et de la pièce en forme de croissant de centre de gravité G.
Le point G1 est alors le centre de gravité des points G et G2 pondérés.
Les points G1 et G2 pouvant par ailleurs être localisés, la relation ci-dessus permet de localiser le point G.
JP et Priam présentent deux manières différentes mais équivalentes de trouver la position de G.
Je te donne ci dessous la relation à obtenir.
A toi de la retrouver en utilisant celles des deux manières qui aura ta préférence :
J'appelle, conformément à mon schéma :
G1 le centre de gravité du petit demi-disque et S1 l'aire de ce demi-disque.
G2 le centre de gravité du grand demi-disque et S2 l'aire de ce demi-disque.
Tu ne pourras pas retrouver la relation que je t'ai donnée tant que tu ne maitriseras pas le cours sur les centres de gravité ( ou les barycentres ).
A toi d'étudier cette question.
On a donc :
avec R=15cm, r=5cm on trouve
Sauf erreur de calcul ....
A mon avis, le contenu de ce cours est très insuffisant pour répondre à la question de la position du centre de gravité.
Je ne vois pas d'autre moyen pour répondre à cette question.
Tout au plus peut on "zapper" la contrainte de l'énoncé qui impose un résultat général et passer directement à l'application numérique.
Puisque S1= 39,27 cm²
= 2,12 cm
S2=353,4 cm²
=6,37cm
Je ne vois pas d'autre moyen pour répondre à cette question.
Je viens de me rendre compte qu'on peut aussi trouver la position du centre de gravité en appliquant le théorème de Guldin !
Voici une autre manière, à laquelle je n'avais pas pensé, de résoudre la question de la position du centre de gravité :
Le corps étudié a une aire S égale à π(R²- r²)/2
En le faisant tourner d'un angle α = 2π autour de l'axe X'X il engendre un Volume V=(4π/3)(R³-r³)
D'après le théorème de Guldin : V = α*d*S ( avec
d=V/ α*S
Si tu finis le calcul tu verras qu'on retrouve le résultat :
Ha voila cette méthode me plaît ! Donc ont reprend tout d'abord il faut les formules générales, comment arrive a cet relation .?
Ha voila cette méthode me plaît ! Donc ont reprend tout d'abord il faut les formules générales, comment arrive a cet relation
Si tu te donnais la peine de lire attentivement mes explications (04-07-18 à 16:15) tu verrais que j'ai déjà fourni la réponse à cette question.
Par application du théorème de Guldin tu obtiens :
avec V=(4π/3)(R³-r³)
α = 2π
S = π(R²- r²)/2
Donc
Rien. il semble que je me sois trompé en pensant que le message du 04-07-18 à 17:34 était une de tes réponses parce que elle commençait par "oui vu desole ..."
C'est exact.
On retrouve le résultat obtenu par l'autre méthode, mais ici l'utilisation du théorème de Guldin permet d'arriver au résultat plus rapidement.
Comment se fait il que oliver383 se métamorphose en Echo05 ?
parce que oliver1383=Echo05=echo05
Ha merci echo05 !
vraiment pas glorieux....


donc oliver1383, tu es prié de fermer ce 2e compte que tu viens de réouvrir...
(modérateur)