Inscription / Connexion Nouveau Sujet
Calorimetrie
Salut à tous je voudrais de l'aide svp :
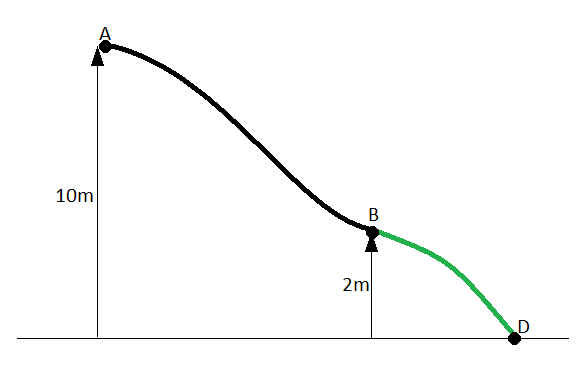
Un morceau de plomb part du repos en un point A situé au sommet d'une pente courbe,glisse le long de la pente sans frottements significatifs quitte la pente en un point B et adopte le mouvement d'un projectile libre soumis à la seule influence de la pesanteur puis vient finalement toucher le sol au point D où il s'arrête. L'altitude du point A ZA=10m celle du point B ZB=2m
1)Calculer la vitesse du morceau de plomb lorsqu'il quitte la pente au point B
2)On admet qu'au point d'impact avec le sol toute l'énergie mécanique du plomb se transforme en énergie calorifique. Calculer l'élévation de température du plomb en supposant que 80% de l'énergie calorifique produite sert à échauffer le plomb
Chaleur massique du plomb*c =128J/Kg.K ;g=9.8m/s2
Bonjour,
Pour avoir de l'aide il me faudrait savoir où tu en es de tes recherches.
La question 1 est une application directe du cours concernant la conservation de l'énergie mécanique.
Merci.
1)Calculons la vitesse Vb
TEM entre A et B en supposant que Va =0m/s puisque c'est le point de repos
On aura :
Frottement négligeable l'énergie mécanique se conserve :
Em(B)=Em(A)
Ep(B)+Ec(B)=Ep(A) >>> mgzb +1/2mvb2= mgza >>> Vb=
((2g(Za -Zb))
T.Bien ( à condition de préciser qu'on choisit de prendre l'origine des énergies potentielles au niveau du sol )
Il ne manque que le résultat numérique présenté avec son unité et un nombre convenable de chiffre significatifs.
Pour la question 2 j'ai compris qu'il faut calculer l'énergie mécanique au point D et que cet même énergie est l'énergie calorifique .Je me dis aussi que les 80% n est rien d'autre que la quantité de chaleur qu'il faut et qui est égal à 80/100 Énergie calorifique
L'énoncé précise qu'au point d'impact avec le sol toute l'énergie mécanique du plomb se transforme en énergie calorifique.
Puis ce même énoncé indique que 80% de l'énergie calorifique produite sert à échauffer le plomb
Oui, c'est en tout cas, ce qui est supposé par l'énoncé (question 2)
Une partie de cette énergie calorifique sert à élever la température du morceau de plomb.
odbugt1 les 80% alors..Du coup l'énergie calorifique est égal la somme de l'énergie mécanique en A et D ou bien ?
Mais comment l'utiliser après
Pas de frottements entre A et D donc Em(D) = Em(A)
D'autre part l'énoncé indique que Em(D) = Ecal et que l'énergie servant à élever la température du Plomb = 80% de Ecal
Tout cela a déjà été exposé dans mon post du 13-03-22 à 19:26
Ec(A) = 0 ( Car en A le morceau de plomb est au repos )
Ep(A) = m * g * zA ( le niveau zéro des énergies potentielles est pris au niveau du sol )
Em(A) = Ec(A) + Ep(A) = 0 + m * g * zA = m * g * zA
Em(D) = Em(A) car pas de frottements entre A et D
Em(D) = m * g * zA
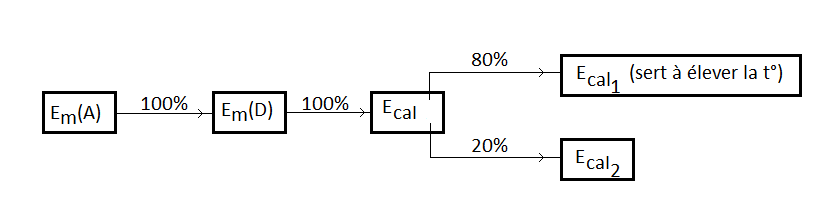
Ecal = Em(D) ( car l'énoncé dit qu'il en est ainsi )
Ecal = m * g * zA
Ecal1 = 80% (Ecal) = 0,8 * Ecal ( ici aussi c'est l'énoncé qui le dit )
Ecal1 = 0,8 * m * g * zA
On peut aussi exprimer Ecal1 en fonction de la chaleur massique du Plomb et de son élévation de température.
Ecal1 = .............................. ( Voir ton cours)
En égalant les deux expressions de Ecal1 , la masse disparait du calcul et on trouve la réponse à la question posée.
= 0.8gza/C >>> 0.8×9.8×10/128 =0.61K
Ton résultat en Kelvin est exact, mais il est plus "parlant" en l'exprimant en °C
La chaleur massique du plomb est exprimée dans l'énoncé en J . kg-1 . K-1 mais elle aurait pu être exprimée
en J . kg-1 °C-1
En effet : 1 J . kg-1 . K-1 = 1 J . kg-1 °C-1
Une différence de 1K est égale à une différence de 1°C
Annuler
connectez vous