Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

Calcul du travail

Posté par
Howard75 10-01-23 à 18:52

Bonsoir à toutes et à tous 🙂

J'aimerais savoir si les réponses que je propose à l'exercice suivant sont bonnes ou non.
Je précise qu'il s'agit d'un exercice de Mathématiques appliqué à la Physique s'appuyant en grande partie sur le concept de produit scalaire.

Merci à ceux qui prendront le temps de me lire et d'éventuellement me corriger 😁

ÉNONCÉ DE L'EXERCICE

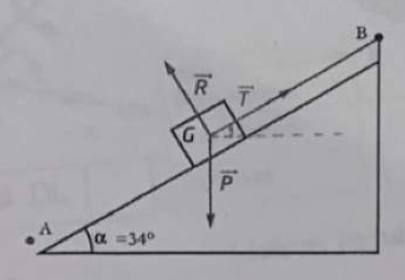
Un colis est tiré par un câble d'un point A à un point B distants de 20 m.
Le plan est incliné de 34°.
Ce colis est soumis à 3 forces \vec{P}, \vec{R} et \vec{T}.

\vec{P} a pour intensité 200 N et est dirigé vers le bas.
\vec{T} a pour intensité 170 N et a les mêmes direction et sens que \vec{AB}
\vec{R} a une direction perpendiculaire au déplacement

Calculer le travail de chaque force \vec{P}, \vec{T} et \vec{R} dans le déplacement de A jusqu'à B.

Rappel : Le travail d'une force \vec{F} dans un déplacement de A jusqu'à B est égal à \vec{F} \cdot \vec{AB}.

MES RÉPONSES

Le travail de la force \vec{T} dans le déplacement de A jusqu'à B est égal à :

\vec{T} \cdot \vec{AB} = \left\lVert \vec{T} \right\rVert \times \left\lVert \vec{AB} \right\rVert \times cos(\widehat{\vec{T}, \vec{AB}}) = 170 \times 20 \times cos(0) = 3400 \text{ J}

Le travail de la force \vec{P} dans le déplacement de A jusqu'à B est égal à :

\vec{P} \cdot \vec{AB} = \left\lVert \vec{P} \right\rVert \times \left\lVert \vec{AB} \right\rVert \times cos(\widehat{\vec{P}, \vec{AB}}) = 200 \times 20 \times cos(90 + \alpha) = 200 \times 20 \times cos(124) \approx -2236,77 \text{ J}

Le travail de la force \vec{R} dans le déplacement de A jusqu'à B est égal à :

\vec{R} \cdot \vec{AB} = \left\lVert \vec{R} \right\rVert \times \left\lVert \vec{AB} \right\rVert \times cos(\widehat{\vec{R}, \vec{AB}}) = \left\lVert \vec{R} \right\rVert \times 20 \times cos(90) = 0 \text{ J}

Calcul du travail

Posté par
hdiallore : Calcul du travail 10-01-23 à 21:30

Bonjour,

Oui, tu as tout trouvé !

Remarque : le travail du poids dépend de la différence d'altitude entre les points de départ et d'arrivée.
• W(\vec P) = mgh si le corps descend
•  W(\vec P) = -mgh si le corps monte
h  est la différence d'altitude entre A et B

A mon avis, c'est plus simple !

Posté par
Howard75re : Calcul du travail 10-01-23 à 21:44

Merci hdiallo pour ta réponse rapide.

L'exercice est à aborder d'un point de vue mathématique. Je ne dois pas recourir aux formules qu'on utilise en Physique pour le calcul du travail mais uniquement passer par le produit scalaire.

Ma réponse pour le calcul du travail de la force P dans le déplacement du colis de A jusqu'à B est-il malgré tout correct ?

Cela me surprend et à la fois pas tant que ça d'obtenir une valeur négative pour le travail du poids car lorsqu'on fait monter l'objet, le poids exerce une forme de résistance (exprimée justement par une valeur négative).

Puis-je selon toi laisser ma réponse en l'état ?

Merci de ton aide ! 😁

Posté par
hdiallore : Calcul du travail 10-01-23 à 23:47

Citation :
L'exercice est à aborder d'un point de vue mathématique.
Non, la mathématique est un simple outil de travail en physique, pour résoudre les équations

Citation :
Je ne dois pas recourir aux formules qu'on utilise en Physique pour le calcul du travail
La formule pour le calcul du travail d'une force constante est mathématique,  mais la signification du travail d'une force est physique

Citation :
Ma réponse pour le calcul du travail de la force Pdans le déplacement du colis de A jusqu'à B est-il malgré tout correct ?
Oui, mais c'est un coup de chance ! Le travail du poids est indépendant du chemin suivi. Il ne dépend que de la différence d'altitude entre le point de départ et le point d'arrivée.

Pour un déplacement du poids de A à B, son travail vaut :

W(\vec P) = mg(Z_A - Z_B)

Le point A étant plus bas que le point B, ZA < ZB ZA - ZB < 0
ZA et ZB sont respectivement les côtés de A et B sur un axe vertical (OZ) orienté vers le haut.

NB : tu peux aussi trouver le travail du poids pour ce cas en utilisant ses composantes \vec P_x et \vec P_y

Il suffit de poser : W(\vec P) = W(\vec P_x) + W(\vec P_y)
Or W(\vec P_x) = ? et W(\vec P_y) = ?

Citation :
Puis-je selon toi laisser ma réponse en l'état ?
C'est un coup de chance qui t'a aidé à tomber sur le bon résultat

Calcul du travail

Posté par
hdiallore : Calcul du travail 10-01-23 à 23:51

Je rectifie un mot, dans mon message précédent.

ZA et ZB sont respectivement les côtes de A et B sur un axe vertical (OZ) orienté vers le haut.

Posté par
Howard75re : Calcul du travail 11-01-23 à 00:32

Citation :
Non, la mathématique est un simple outil de travail en physique, pour résoudre les équations


J'ai bien compris ta remarque et je suis évidemment d'accord, les mathématiques sont un outil qu'on utilise en Physique 👍

Ce que je voulais dire c'est qu'ici il ne s'agit en réalité pas d'un exercice de Physique mais de Mathématiques et la consigne est d'utiliser le produit scalaire des 2 vecteurs afin de calculer le travail de chaque force (y compris celui du poids).

Sinon, en appliquant purement la formule "physique", je peux trouver un résultat positif et même la masse du colis et l'altitude entre le point A et le point B :

P = m \cdot g
m = \frac{P}{g}
m = \frac{200}{9,8} \approx 20,41 kg
sin(34) = \frac{h}{AB} = \frac{h}{20} \implies h = 20sin(34) = 11,18 \text{ m}

Enfin en regroupant tout ça j'obtiens :

W_{AB}(\vec{P}) = -mgh = -mg(z_{A} - z_{B}) (car le colis monte)
W_{AB}(\vec{P}) = -20,41 \times 9,8 \times (0 - 11,18) =
W_{AB}(\vec{P}) \approx 2236,20 \text{ J}

Du coup, je ne comprends pas si j'ai bon quand j'obtiens une valeur négative via le produit scalaire des deux vecteurs.

Posté par
Howard75re : Calcul du travail 11-01-23 à 00:43

hdiallo @ 10-01-2023 à 21:30


Remarque : le travail du poids dépend de la différence d'altitude entre les points de départ et d'arrivée.
• W(\vec P) = mgh si le corps descend
•  W(\vec P) = -mgh si le corps monte
h  est la différence d'altitude entre A et B

A mon avis, c'est plus simple !


En poursuivant dans cette logique, peu importe que le colis monte ou descende la formule qui correspond renvoie toujours une valeur du travail du poids positive.

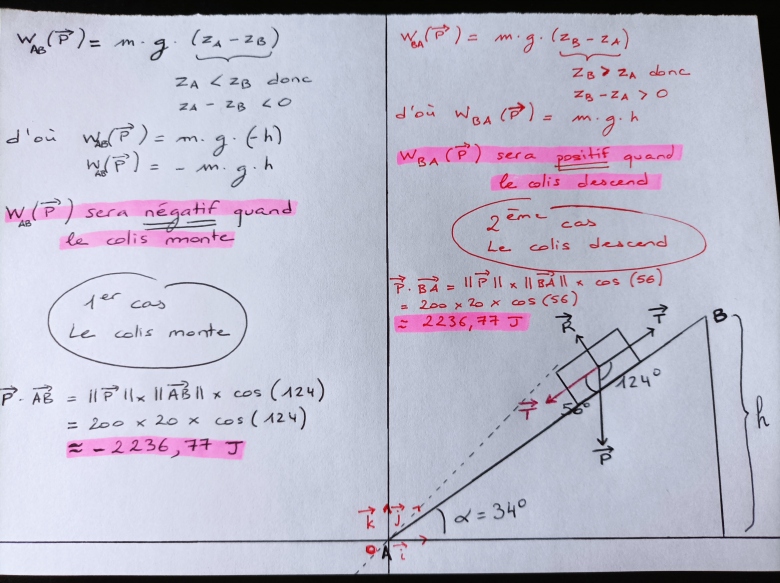
1er cas : Le colis monte
m et g sont des valeurs positives
h est négatif car z_{A} - z_{B} < 0
donc W = -mgh est positif

2eme cas : Le colis descend
m et g sont des valeurs positives
h est positif car z_{B} - z_{A} > 0
donc W = mgh est positif

Je ne comprends donc pas pourquoi le produit scalaire, lui, renvoie une valeur négative et par conséquent la signification du résultat.

D'où vient l'erreur (si c'en est une) avec l'approche du produit scalaire des 2 vecteurs ? 🤔

Posté par
hdiallore : Calcul du travail 11-01-23 à 01:47

Tu n'as pas bien compris mon message, ou alors j'explique mal , donc je reprend :

Ton colis va de A vers B. Le travail du poids est, dans ce cas : W(\vec P) = mg (Z_A-Z_B)
Où ZA - ZB = - h (pour ce cas présent, car l'altitude augmente au cours de la montée)
Alors  W(\vec P) = -mgh

Remarque: le travail du poids \vec P d'un corps pour un déplacement d'un point A à un point B peut aussi s'écrire : W(\vec P) = \vec P.\vec {AB}
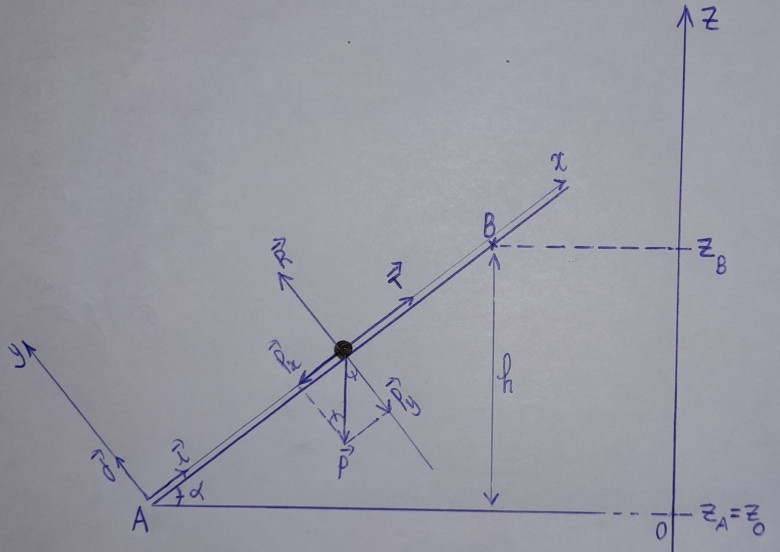
En projetant les vecteurs \vec P et \vec {AB} dans un repère (O, \vec i, \vec j , \vec k)  avec \vec k vertical ascendant, tu obtiens :

\vec P (0, 0, -mg)
\vec {AB}(x_B - x_A ; y_B - y_A; z_B - z_A)

Alors, pour avoir le travail du poids, tu fais juste la multiplication des deux coordonnées de ces deux vecteurs sur l'axe Oz, puisque P_x = 0 et  P_y = 0
Donc W(\vec P) = \vec P.\vec {AB}= - mg.(z_B - z_A) = mg(Z_A - Z_B)

On comprend aisément que la relation  W(\vec P) = \vec P.\vec {AB}= - mg.(z_B - z_A) = mg(Z_A - Z_B) est l'application du produit scalaire de deux vecteurs.

Posté par
vanoisere : Calcul du travail 11-01-23 à 10:41

Bonjour à tous

Citation :
Puis-je selon toi laisser ma réponse en l'état ?

Je réponds "oui" à cette question. Au début du programme de mécanique en première, le travail d'une force constante au cours d'un déplacement rectiligne du point d'application est défini comme le produit scalaire des vecteurs force et déplacement, ce qu'a parfaitement faitHoward75 dans son message du  10-01-23 à 18:52. Les autres méthodes sont introduites plus tard, lorsque l'énergie potentielle est définie.

Posté par
Howard75re : Calcul du travail 11-01-23 à 11:49

Re-bonjour à toutes et à tous 🙂

Je pense avoir compris 🤯 Si vous me dites que c'est bon, je clos le sujet.

J'ai repris le cas précédent et son cas contraire où le colis descend sur le même tapis roulant en subissant une force de traction \vec{T} dans la même direction mais dans le sens contraire.

- Lorsque le colis passe du point A au point B (et donc monte) sur un tapis roulant incliné à 34° par rapport à l'horizontale, le travail du poids noté W_{AB}(\vec{P}) est négatif ce que le produit scalaire renvoie très bien
- Lorsque le colis passe du point B au point A (et donc descend) sur le même tapis roulant incliné à 34° par rapport à l'horizontale, le travail du poids noté W_{AB}(\vec{P}) est positif ce que le produit scalaire renvoie également très bien

Ceci s'interprète de la manière suivante :

- Lorsque le colis passe du point A au point B, le poids du colis agit comme une forme de resistance à son élévation, ce qui explique la valeur négative qu'on obtient
- Lorsqu'au contraire le colis passe du point B au point A, le poids du colis agit comme une forme "d'aide", ce qui explique la valeur positive qu'on obtient

Pour reprendre les propos de vanoise, c'est le principe de l'énergie potentielle : on dépense de l'énergie pour monter l'objet et ensuite on a besoin de moins d'énergie pour le faire redescendre car le poids de l'objet nous y aide.

Et donc il n'est pas incohérent d'avoir une valeur du travail du poids négative quand il monte et positive quand il descend.

C'est ça ?

Voici une petite image qui récapitule ces 2 scénarios et les calculs associés qui illustre ce changement de signe dans le calcul du travail du poids en fonction de si le colis monte ou descend.

Merci à toutes et à tous pour votre aide 😁

Calcul du travail

Posté par
Howard75re : Calcul du travail 11-01-23 à 11:54

Howard75 @ 11-01-2023 à 11:49


- Lorsque le colis passe du point B au point A (et donc descend) sur le même tapis roulant incliné à 34° par rapport à l'horizontale, le travail du poids noté (petite correction ici 👉) W_{BA}(\vec{P}) est positif ce que le produit scalaire renvoie également très bien


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 237 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !