Inscription / Connexion Nouveau Sujet
Calcul des angles
Bonjour à tous j'avais un exercice dont ça fait des jours que je suis sur la même question j'aimerai bien que vous m'y aidez:
L'exercice comporte une figure j'ai ainsi vu un exercice identique sur le net par conséquent j'aimerai bien vous redirigé sur ce site: ** lien vers l'énoncé effacé **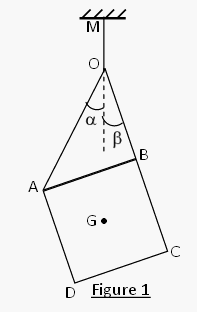
C'est l'exercice 3 disant: Une plaque carré homogène ABCD de masse M=10kg, de centre......
Je me suis bloqué au niveau de la question 3.2 disant de déduire les angles alpha et beta formés respectivement pas les fils OA et OB avec la verticale au point O.
Merci de votre aide
Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum 
![]()
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
Désolé dans l'exercice les angles ne sont pas marqué. Les donnés sont alpha= 31,1 degres et beta= 21,8. Alpha se trouvant à gauche et beta à droite.
Je suis vraiment désolé j'ai un problème pour construire la figure c'est pourquoi j'ai procédé ainsi.
Bonjour.
Si les valeurs des angles  sont données, quelle est la question ?
sont données, quelle est la question ?
Précisez donc votre énoncé.
A plus.
Bonjour voilá l'énoncé:
Une plaque carré homogène ABCD de masse M=10kg, de gravité G, est supporté, comme l'indique la figure, par les fils AO et BO, liés en O au fil OM, M étant un point fixe.
Les fils sont tous de masse négligeables. On donne AB=c=20cm, OB=b=15cm, OA=a=25cm.
3.1 En considérant l'ensemble AOBCD comme un solide unique, montrer que le fil OM est vertical lorsque le système est en équilibre.
Calculer la Tension de ce fil. On donne g=10N/kg
3.2 Montrer que le triangle AOB est rectangle en B.
En déduire les angles  et
et  formés respectivement par les fils OA et OB avec la verticale au point O.
formés respectivement par les fils OA et OB avec la verticale au point O.
3.3 Calculer les intensités des tensions des fils OA et OB en prenant pour valeur  =31.3 et
=31.3 et  =21.8
=21.8
A la fin de l'exercice, il peut arriver que la valeur des angles différe á cause des arrondis c'est pour on nous a précisé les angles. Mais il faut les calculer d'abord. Merci d'avance
Désolé Edit Coll c'est que c'est la première fois que je poste un exercice ayant une figure. Mais sache que ça ne se répétera plus.
Bonjour,
D'accord...
__________
Je te signale que tu as mal recopié la valeur attendue de l'angle  dans ton message du 14 à 16 h 45
dans ton message du 14 à 16 h 45
Les valeurs approchées étant :

 21,80141°
21,80141°

 31,32869°
31,32869°
Mais je te laisse avec picard 

...
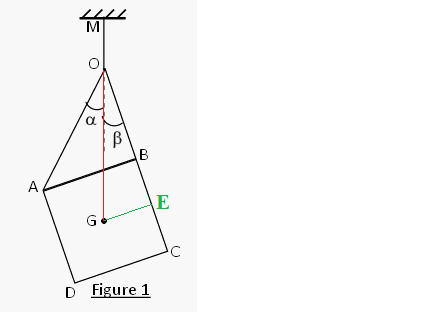
GE = OE.tg(Beta)
(1/2).AB = (OB + BE).tg(Beta)
(1/2).AB = (OB + (1/2).AB).tg(Beta)
10 = (15 + 10)*tg(Beta)
tg(Beta) = 10/25
Beta = 21,801° (arrondi)
AB = OB.tg(alpha + Beta)
20 = 15*tg(alpha + Beta)
tg(alpha+Beta) = 20/15
alpha+Beta = 53,130°
Alpha = 53,130 - 21,801 = 31,329° (arrondi)

Salut Coll, Salut RangerB.
3.1 En considérant l'ensemble AOBCD comme un solide unique, montrer que le fil OM est vertical lorsque le système est en équilibre.
Calculer la Tension de ce fil. On donne g=10N/kg
A quelles forces la plaque est-elle soumise ? Quelle condition doivent vérifier ces forces pour qu'il y ait équilibre ?
3.2 Montrer que le triangle AOB est rectangle en B.
Comment en géométrie montre-t-on qu'un triangle est rectangle ? Indice, ça commence par Py... et ça finit par ...ore !
Pour ce qui est du calcul des angles
 et
et  , il faut appliquer les relations trigonométriques dans le triangle quelconque, c'est un peu laborieux et je ne suis pas certain qu'elles soient connues au niveau de la classe de seconde.
, il faut appliquer les relations trigonométriques dans le triangle quelconque, c'est un peu laborieux et je ne suis pas certain qu'elles soient connues au niveau de la classe de seconde.
Je n'ai pas trop le temps ce matin, mais j'y reviens en fin d'après midi.
En ce qui concerne la dernière question, est ce qu'une solution graphique ne suffirait pas ?
Sinon, il faut passer par les projections.
Désolé, je dois partir maintenant.
A tout à l'heure.
Oubliez ce que j'ai dit à la fin de mon précédent message, la méthode proposée par J-P est bien plus simple que ce à quoi j'avais pensé dans mon esprit embrumé.
Au revoir.
Bonsoir à tous et merci à tous ceux qui ont pris la peine de m'aider. Dans l'exercice j'ai réussi à traiter les questions suivantes:
3.1 Si le système est en équilibre alors on obtiendra 2 forces qui sont directement opposés: la tension du fil et le poids. Or on a le poids qui est toujours dirigé vers le bas et sa direction est la verticale donc (OM) étant la droite qui supporte le vecteur T est verticale.
ON a T=P=mg = 10kg 10N/kg = 100N
10N/kg = 100N
3.2 Pour montrer que ABO est rectangle. J'ai utilisé comme l'a dit Piscard, la réciproque du théorème de Pythagore.
Et pour la déduction j'ai utilisé la methode de J-P( ).
).
3.3 Ici j'ai utilisé la méthode par calcul en traçant un repère d'origine O et dont l'axe des ordonnés est confondu à (OM). Ensuite je me suis dit que la somme des tensions des fils (OA) et (OB) est égale à celle de (OM). D'ou l'on peut établir la relation suivante: vecT+ vecT1+ vecT2=0
Ensuite en appliquant cette relation; j'ai fait les projections suivant l'axe des x et des y. Cependant j'ai obtenue à la fin des égatilés que je ne peut pas simplifié je ne sais pas là ou y'a erreur j'espère que vous allez m'y aider. J'ai obtenu:
Suivant(x): -Sin T1+Sin
T1+Sin T2=0
T2=0
Suivant(y): -Cos T1-Cos
T1-Cos T2+T=O
T2+T=O
Merci d'avance
sin(31,3°).T1 = sin(21,8°).T2
-cos(31,3°).T1 - cos(21,8°) + 100 = 0
Simple système de 2 équations à 2 inconnues qui résolu donne :
T1 = 46,4 N
T2 = 65,0 N



