Inscription / Connexion Nouveau Sujet
Calcul angle... fibre optique (loi de descarte)
Bonjour,
Voila j'ai un petit DM a faire pour mardi et je ne comprend pas quelque questions voici :
Info donnée de l'exo fibre optique ici :
Gaine : N2 = 1.40
Cœur : N1 = 1.49
i1 = 30° (rayon incident)
Air n = 1 (A)
Calculer L'angle de réfraction en A :
D'après moi la réponse doit être : n1 x Sin i1 = n2 sin i2
soit : 1 x sin(30) = 1.40 x sin i2
sin i2 = 1 x sin(30) / 1.40 = 0.36 donc Arcsin(0.36) = 21.10°
Cela est juste ?
Calculer L'angle limite d'incidence du rayon lumineux à la surface de séparation coeur-gaine :
D'après moi la réponse soit être : n1 x Sin i1 = n2 sin i2
soit : 1 x sin i1 = 1.40 x sin(21.10)
sin i1 = 1.40 x sin(21.10) / 1 = 0.50 donc Arcsin(0.50) = 30°
Cela est juste ?
Après c'est la que sa se complique pour moi :
- Calculer L'angle limite a la surface de séparation coeur gaine
- Pour la propagation d'un rayon lumineux dans la fibre, l'angle d'incidence doit etre inferieur à la valeur de l'angle 0, donnée par la relation sin 0 = Racine carrée de n1² - n2² , Calculer 0.
- Comparer les valeurs de i1 et de 0.
Merci de m'éclairer. 
1° Où est le point A ? N'est-il pas situé sur l'extrémité du coeur ?
2° et 3° : je ne saisis pas la différence entre les deux questions.
1)
En supposant que A se trouve à l'entrée de la fibre sur l'interface air-coeur fibre.
n(air).sin(i) = n1.sin(r)
1 * sin(30°) = 1,49 * sin(r)
sin(r) = 0,33557
r = 19,6°
-----
2)
n1.sin(i1) = n2.sin(i2)
1,49*sin(i1) = 1,40.sin(i2)
sin(i2) = (1,49/1,40) * sin(i1)
et donc : (1,49/1,40) * sin(i1) < 1
sin(i1) < 1,40/1,49
sin(i1) < 0,93959...
i1 < 70°
L'angle limite d'incidence du rayon lumineux à la surface de séparation coeur-gaine est 70°
-----
Essayer de comprendre ce qu'on fait avant de se lancer dans des calculs en appliquant des formules apprises par coeur.
Le but de la fibre est de propager le rayon le long de la fibre, il faut donc empêcher la réfraction au nineu de l'interface coeur-gaine.
Il faut donc éviter le cas du dessin du haut, et il faut se retrouver dans le cas du dessin du bas.
Pour cela, il faut donc qu'il y ait REFLEXION totale au niveau des interfaces coeur-gaine.
-----
3)
Quelques explications :
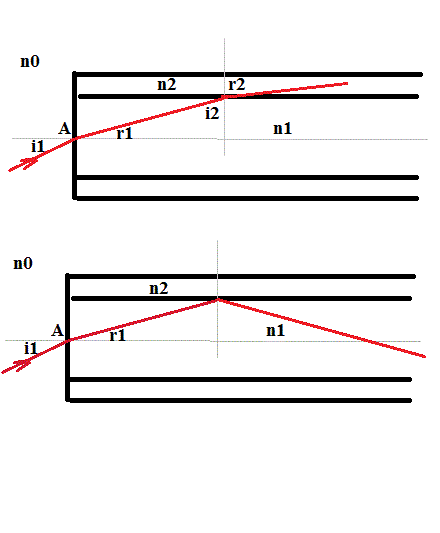
On a les 3 relations (avec les notations du dessin du haut):
n0.sin(i1) = n1.sin(r1)
i2 = 90° - r1
n1.sin(i2) = n2.sin(r2)
soit donc (relation 3): sin(r2) = (n1/n2).sin(i2)
Si on veut que la réfraction soit impossible et donc avoir une réflexion totale aux interfaces coeur-gaine, il faut donc que (n1/n2).sin(i2) >= 1 (ce qui rend impossible une valeur pour sin(r2))
(n1/n2).sin(i2) >= 1
(n1/n2).sin(90°-r1) >= 1
(n1/n2).cos(r1) >= 1
cos(r1) >= n2/n1
cos²(r1) >= n2²/n1²
or sin(r1) = (n0/n1).sin(i1)
sin²(r1) = (n0/n1)².sin²(i1)
cos²(r1) = 1 - sin²(r1) = 1 - (n0/n1)².sin²(i1)
1 - (n0/n1)².sin²(i1) >= n2²/n1²
et comme no = 1 (air) -->
1 - (1/n1)².sin²(i1) >= n2²/n1²
(n1² - sin²(i1))/n1² >= n2²/n1²
(n1² - sin²(i1)) >= n2²
sin²(i1) <= n1² - n2²
sin(i1) <= V(n1² - n2²) (avec V pour racine carrée).
Avec theta la valeur max de i1 pour avoir une réflexion totale aux interfaces coeur-gaine, on a donc: sin(theta) = V(n1²-n2²)
Avec les valeurs numériques de l'énoncé, on a donc sin(theta) = V(1,49² - 1,4²) = 0,51
et theta = 30,66°
So i1 < theta, il y a réflexion totale aux interfaces coeur-gaine
Avec i1 = 30°, on a bien i1 < theta --> il y a réflexion totale aux interfaces coeur-gaine (et donc une bonne transmission du rayon dans la fibre).
-----
Rien relu ... 


