Inscription / Connexion Nouveau Sujet
Barre en mouvement
Bonjour,
Je rencontre un problème dans un exercice de physique.
Y aurait-il quelqu'un pour m'aider?
Voici le sujet de l'exercice: 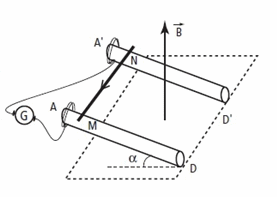
** énoncé effacé ; image laissée **
Voici ce que j'ai fait:
1) Faire le bilan des forces appliquées à la tige MN.
Les forces appliquées à la tige MN sont :
- son poids P
- la force R exercée par les rails
- la force B électromagnétique
- la force F de Laplace.
2) Déterminer, au cours du déplacement d de la tige MN, l'expression littérale des travaux des forces appliquées à la tige MN, en fonction de l'intensité de la force, de d, de g et de l'angle α.
L'expression littérale des travaux des forces appliquées à la tige MN s'exprime par :
WP = mg ( zA - zB)
WR = 0 car la direction de est perpendiculaire au déplacement.
WB = kI
WF = IlB sin α
est-ce bon?
3) En appliquant le théorème de l'énergie cinétique à la tige MN, sur le déplacement d, donnez l'expression littérale, en fonction de m, g et de l'angle α, de la force de Laplace, puis calculer sa valeur numérique.
Le théorème de l'énergie cinétique : Entre deux positions A et B, dans un référentiel galiléen, la variation d'énergie cinétique d'un solide en translation est égale à la somme des travaux des forces extérieures.
Ici, je ne vois pas comment il faut procéder.
Merci d'avance à tous ceux qui pourront m'aider.
Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum 
![]()
Je vois que l'énoncé ne paraît pas, donc je la remets:
Deux rails parallèles AD et AD' dsitant de l, sont disposés selon des lignes de plus grande pente faisant un angle  avec le plan horizontal.
avec le plan horizontal.
Les deux rails sont reliés à un générateur électrique G par l'intermédiaire de fils conducteurs; le circuit est fermé par une tige MN de masse m qui glisse sans frottements en M et N sur les rails en restant horizontal.
Le circuit est parcouru par un courant continu d'intensité I indépendant de la position de la tige; le sens du courant est indiqué sur le schéma.
Les rails sont placés dans une région de l'espace où existe un champ magnétique uniforme vectB vertical dirigé ers le haut.
Données:
l = 12cm I - 2,0 A
m 32g  = 8°
= 8°
g - 9,8N.Kg-1
Questions:
1) Faire le bilan des forces appliquées à la tige MN.
2) Déterminer, au cours du déplacement d de la tige MN, l'expression littérale des travaux des forces appliquées à la tige MN, en fonction de l'intensité de la force, de d, de g et de l'angle α.
3) En appliquant le théorème de l'énergie cinétique à la tige MN, sur le déplacement d, donnez l'expression littérale, en fonction de m, g et de l'angle α, de la force de Laplace, puis calculer sa valeur numérique.
4) En déduire la valeur B du champ magnétique
bonsoir,
Pour 1
Le champ magnétique B n'est pas une force
Les forces appliquées à la tige MN sont :
- son poids P
- la force R exercée par les rails
- la force F de Laplace.
Pour 2
WP = m g d sin (il n'y a que P sin
(il n'y a que P sin qui travaille)
qui travaille)
WR = 0 (perpendiculaire au déplacement)
WF = - I d B cos (il n'y a que F cos
(il n'y a que F cos qui travaille et il est négatif parce F est opposée au déplacement (travail résistant))
qui travaille et il est négatif parce F est opposée au déplacement (travail résistant))
Fais un schéma. Si tu ne comprends pas, je ferai un schéma...
Oui merci j'ai compris.
Donc voilà ce que j'ai finalement mis:
1) Faire le bilan des forces appliquées à la tige MN.
Les forces appliquées à la tige MN sont :
- son poids P
- la force R exercée par les rails
- la force F de Laplace.
2) Déterminer, au cours du déplacement d de la tige MN, l'expression littérale des travaux des forces appliquées à la tige MN, en fonction de l'intensité de la force, de d, de g et de l'angle α.
L'expression littérale des travaux des forces appliquées à la tige MN s'exprime par :
Le travail du poids s'exprime ici par :
WP = m g d sin α
WR = 0 car la direction de est perpendiculaire au déplacement.
Les forces de Laplace s'exprime par : F = I l B sin α
Donc WF = F*d soit - I d B sin α (négatif car le direction est de sens opposé au déplacement).
3) En appliquant le théorème de l'énergie cinétique à la tige MN, sur le déplacement d, donnez l'expression littérale, en fonction de m, g et de l'angle α, de la force de Laplace, puis calculer sa valeur numérique.
Le théorème de l'énergie cinétique : Entre deux positions A et B, dans un référentiel galiléen, la variation d'énergie cinétique d'un solide en translation est égale à la somme des travaux des forces extérieures.
De plus, l'énergie électrique peut se convertir en énergie mécanique et inversement.
Or et = WR + WF .
Nous pouvons donc en conclure que le travail de la force de Laplace est égale au travail du poids
Donc WP + WR = WF
Comme WR = 0, WP = WF
WP = m g d sin α
WF = I d B sin α
Donc F = m g sin α.
Les données :
m = 32,0g = 0,032kg
g = 9,8N.kg-1
α = 8°
Soit l'application numérique :
F = 0,032*9,8*sin 8° = 3,93.10-2 N
On va reprendre les choses une par une...
F = I l B sin α
C'est exact pour la force de Laplace,
 étant l'angle entre I et B. Ici,
étant l'angle entre I et B. Ici, Par contre, pour le travail, comme je l'ai écrit, il n'y a que
Attention, c'est un peu subtil... Il faut un schéma pour comprendre. Je le ferai si c'est indispensable...
OK ?
La force de Laplace est dans l'autre sens.
R est perpendiculaire au plan des rails, pas perpendiculaire au sol.
Je vais faire un schéma.
L'angle "rouge" est à l'angle
"noir" du plan incliné parce que ce sont des angles à côtés perpendiculaires.
L'angle "vert" est à l'angle
"noir" du plan incliné parce que ce sont des angles à côtés parallèles.
1)
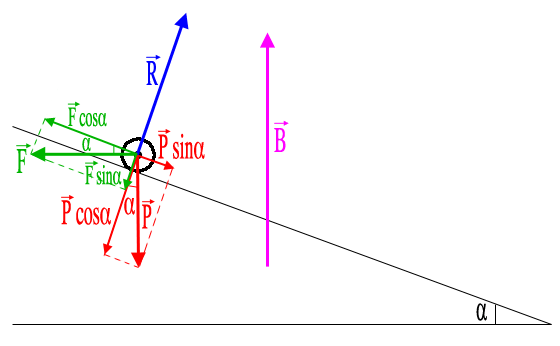
Les forces tout d'abord :
- le poids (vers le bas et perpendiculaire au sol)
- la réaction du support (les rails) perpendiculaire au plan des rails et dirigée vers le haut
- la force de Laplace perpendiculaire au plan contenant I et B (ou le plan contenant la barre et B) et dirigée comme sur le schéma (le sens est donné par les règles connues (ou qui devraient l'être) comme la règle de la main droite).
2)
est perpendiculaire au déplacement donc
.
est perpendiculaire au déplacement donc
.
est perpendiculaire au déplacement donc
.
Les forces qui travaillent sont donc et
.
Je n'ai pas réussi à trouver dans l'énoncé une indication disant que la barre monte ou descend... L'énoncé est -il complet ?
Il y a donc 3 cas possibles :
a) La barre descend le plan incliné
(travail moteur ==> positif)
Pour la force de Laplace :
,
étant l'angle entre I et B. Ici, I (ou la barre) et B sont perpendiculaires donc
.
Donc :
(travail résistant donc négatif).
b) La barre ne bouge pas
Les forces et
sont égales en norme.
Donc :
Le travail est donc nul.
c) La barre monte le plan incliné
(travail résistant ==> négatif)
(travail moteur donc positif).
l est la longueur de la barre et d le chemin parcouru sur le plan incliné.
Des questions ?
Quant à appliquer le théorème de l'énergie cinétique dans la question 3, il doit manquer quelque chose parce que qui dit "énergie cinétique", dit "vitesse"... Or il n'y a aucune indication de vitesse...
Merci bien pour les explications, j'ai mieux compris.
En fait, au point 2, il est dit que la tige MN glisse en remontant sur les rails à vitesse constante.... je viens effectivement de m'apercevoir que je ne l'ai pas mis. Je suis désolée. Donc voilà les éléments qui manquaient.
Merci bien.
En fait, cela correspond au cas b) mais pas comme je l'ai envisagé.
On considère que la barre est en mouvement et on ne s'occupe pas du démarrage...
Donc, si la vitesse est constante, l'accélération est nulle et la somme des forces est donc nulle.
Les forces \vec{P}sin\alpha et \vec{F}cos\alpha sont égales en norme.
Donc :
Comme la barre glisse en remontant, on a :
(travail résistant ==> négatif)
(travail moteur donc positif).
Pour la 3 :
Comme la vitesse est constante,  Ec = 0 et :
Ec = 0 et :
Donc :
Je te laisse calculer la valeur numérique...
Et tu dois pouvoir faire la 4 ?
"Les forces \vec{P}sin\alpha et \vec{F}cos\alpha sont égales en norme." ==> Les forces et
sont égales en norme.


