Inscription / Connexion Nouveau Sujet
Ballon sonde
Un ballon sonde de volume Vb est gonflé à l'hélium. Une nacelle attachée au ballon emporte du matériel scientifique. On modélisera la valeur f de la force de frottement de l'air sur le système {ballon + nacelle} par l'expression : f = K * µ * v² où µ est la masse volumique de l'air et v la vitesse du centre d'inertie du système {ballon + nacelle}. Cette force de frottement a la même direction que le mouvement du ballon, elle est de sens opposé.
Données : µ = 1.22 kg.m¯³ ; Volume du ballon Vb = 9.0m³ ; g=9.81 N.kg¯¹ ; masse du ballon (enveloppe + hélium) m =2.10kg ; masse de la nacelle vide : m' 0.50kg.
1. Condition de décollage du ballon.
a) établir le bilan des forces extérieurs exercées sur le système {ballon + nacelle} lorsque le ballon vient juste de décoller. Sa vitesse étant alors considérées comme nulle.
Pour ce faire définir le système, puis lister chaque force extérieure appliquée en donnant ces caractéristiques.
b) a quelle condition le système {ballon + nacelle} décolle-t-il ?
c) soit m(max), la masse de matériel emporté : A quelle valeur m(max) doit elle être inférieur pour que le ballon décolle ?
2. Force de frottement fluide f lorsque le ballon vole.
a) la masse M de matériel réellement emporté est de M=2.0kg. Lors de son ascension verticale, la vitesse du ballon se stabilise rapidement à la valeur de v=5.0 m.s¯¹. Qualifier le mouvement du système {ballon + nacelle} lors de cette ascension.
b) faire le bilan des forces extérieurs appliqués au système {ballon + nacelle}.
c) utiliser un principe célèbre vu en classe de seconde. En déduire une relation entre les vecteurs forces.
d) tracer un axe orienté oy vers le haut et représenter ces forces qualitativement à partir de l'origine de l'axe.
e) en déduire une relation entre les normes des forces.
f) calculer la valeur K du coefficient de frottement.
Bonjour, est-ce que vous pourriez me donner quelques pistes pour commencer svp?
Merci.
Bonjour,
a.
Au tout début du décollage, la vitesse est nulle donc la force de frottement est aussi nulle.
Il y a donc le poids et la poussée d'Archimède qui s'exerce sur le système.
b. à ton avis ?
a) le système que l'on étudie est {ballon + nacelle}
les forces s'exerçant sur le système sont le poids et la poussé d'Archimède.
Le poids P(b/n)
Point d'application: G
Direction: verticale
sens: vers le bas
Valeur: P=m*g donc 2.10kg*9.81 N.kg¯¹=20.6kg
La poussée d'Archimède Fa
Point d'application: Centre de poussée
Direction: verticale du ballon
Sens: Vers le haut
Valeur: Fa=pVg donc 1.22 kg.m¯³* 9.0m³*9.81 N.kg¯¹ = 107.7
J'ai juste?
b) Quand la vitesse n'est pas nulle.
je mettais posée la question s'il fallait que j'additionne les masse et apparemment oui dsl :s donc P=mg = 2.60kg*9.81 N.kg¯¹ = 25.51Kg
je comprends pas pq tu me dis P et Fa sont en N
Hum :s
Je reprends.
a) le système que l'on étudie est {ballon + nacelle}
les forces s'exerçant sur le système sont le poids et la poussé d'Archimède.
Le poids P(b/n)
Point d'application: G
Direction: verticale
sens: vers le bas
Valeur: P=m*g donc 2.60kg*9.81 N.kg¯¹ = 25.51 N
La poussée d'Archimède Fa
Point d'application: Centre de poussée
Direction: verticale du ballon
Sens: Vers le haut
Valeur: Fa=pVg donc 1.22 kg.m¯³* 9.0m³*9.81 N.kg¯¹ = 107.7N
Les caractéristiques sont juste sinon?
b) le système {ballon + nacelle} décolle seulement si Fa > P.
c) m(max) doit être strictement inférieur à 82.19N pour que le ballon doit décoller. (J'ai fait 107.7-25.51)
Tu confonds les newtons (N) et les kilogrammes (kg)
Fa et P sont des forces en N
m est une masse en kg
Ce que tu me dis est une bonne idée
P' = (107.7 - 25.51) est le poids généré par le matériel de masse m(max)
or P' = m(max).g donc m(max) = P'/g = 82.19/9.81 = ...... kg
Merci.
Donc c)
P'= m(max) * g
donc m(max)=P'/g où P' est le poids du matériel de masse m(max)
m(max)= (107.7-25.51)/9.81 = 8.4kg.
Donc m(max) 8.4kg
8.4kg
2. Force de frottement fluide f lorsque le ballon vole.
a) Le mouvement est rectiligne uniforme.
b) Les forces extérieurs appliquées au système {ballon + nacelle} sont le poids, la poussée d'Archimède et la réaction.
c) Je ne vois pas.
Bon puisque tu es absent je considère que oui.
2.
a. Le ballon a une vitesse qui augmente dans un premier temps : mouvement rectiligne accéléré.
Cependant, plus la vitesse augmente et plus la force de frottement augmente également.
A partir d'un instant, la force de frottement et le poids compensent la poussée d'Archimède : le système atteint alors une vitesse limite : mouvement rectiligne uniforme.
Tu es de retour 
Une force s'exprime toujours en newtons (N).
J'ai l'impression que tu confonds le poids d'un solide et sa masse. Il faut juste retenir cette formule :
P = m.g
m est une masse en kg
g est l'intensité de la pesanteur en N/kg
Donc P est une force (ici une valeur) en N
Hum d'accord, je reverrai qd même ma leçon pour les unités.
II.a). Oui excuse moi je n'ai pas fait attention que c'est marqué lors de l'ascension.
J'ai comprit ce que tu as dit mais pour la force de frottement, le frottement se fait avec l'air?
absolument. Ce que je t'ai dit est pour ta culture personnelle.
Dans ton exercice, on se place déjà au moment où la force de frottement et le poids du système compensent la poussée d'Archimède.
a. Tu as donc raison de dire que le mouvement est rectiligne uniforme.
b. Bilan des forces :
* la force de frottement exercée par l'air sur le système
* le poids du système
* la poussée d'Archimède
Il ne peut pas y avoir de force de réaction car le ballon n'as plus de contact avec le sol...
c. Utilise le principe d'inertie
Oui, justement j'ai trouvé que l'ensemble de force s'annule donc comme tu m'as dit vect f+Fa+P=0, et vect f+p=-Fa, je pense que la relation entre les vecteurs forces c'est que le frottement + le poids compense la poussée d'Archimède.
Oki dsl.
Je comprends pas l'axe orienté vers le haut, c'est pas un axe comme en math qui faut faire?
C'est un axe pour pouvoir projeter les vecteurs dessus.
En effet, si la force a le même sens que l'axe il y aura un +
sinon un -
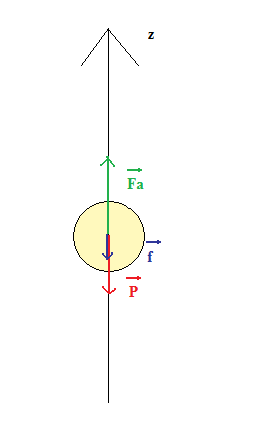
Oké.
Pr les vecteurs, il faut prendre une échelle à partir des valeurs qu'on avait donc P= 25.51 N et Fa=107.7N ?
Okay.
Donc pour la e) la relation entre les normes des forces je ne vois pas du tout.
Sinon pour la f), il faut prendre l'expression qu'on nous a donné ds l'énoncé donc f = K * µ * v² puis faire K = (µ * v²) / f ?
e.
Il faut comme je te l'avais dit projeter la relation sur l'axe z :
donc Fa = P+f
f.
f = K * µ * v²
soit avec e.
f = Fa - P
<=>
K * µ * v² = Fa-P
d'où
K = (Fa-P)/(µ.v^2)
Merci 
On sait que f = K * µ * v² et que Fa = P+f donc f= Fa - P.
On peut donc écrire :
K * µ * v² = Fa-P
donc
K = (Fa-P)/ (µ.v^2)
(107.7-25.51)/(1.22*9.0)=7.5N.m¯¹
Je ne suis pas du tout sur de l'unité.
f = K * µ * v²
v est en m.s-1
donc v2 est en m2.s-2
µ est en kg.m-3
f est en N
donc K = f/(µ.v^2) est en .....



