Inscription / Connexion Nouveau Sujet
Attraction foraine ( Energie mecanique, vitesse...)
Bonjour pouriez vous m'aider a résoudre cet exercice svp ?
Une attraction foraine est constituée d'un rail comportant une boucle circulaire de rayon R. Un palet de masse m, peut glisser sans frottement sur le rail. Le palet peut effectuer la boucle si sa vitesse au sommet est supérieure a gR. L'origine de l'énergie potentielle est prise au niveau le plus bas de la trajectoire en A. Le palet est repéré sur la boucle au point B par l'angle 
.
1. Quelle est l'expression de l'energie mécanique di palet en A ?
Em = Ec + Epp = 1/2mv2 + mg(z-zref) ?
2. Exprimer l'energie mecanique du palet en mouvement dans la boucle (en B) en fonction de sa vitesse v, de R, , m et g.
comment je peux introduire et R dans l'expression ?
3. Pourquoi l'energie mecanique est elle constante ?
4.a. Avec aielle vitesse minimale doit on lancer le palet sur la partie horizontale du rail afin qu'il effectue une boucle ?
b.Calculer cette vitesse pour R=1,5m
Merci d'avance !!
Salut !
1. Ta réponse est correcte mais comme tu sais que l'origine de l'énergie potentielle est prise en A, l'énergie potentielle du palet est nulle en A : . Par contre, ta réponse est juste dans tous les autres cas.
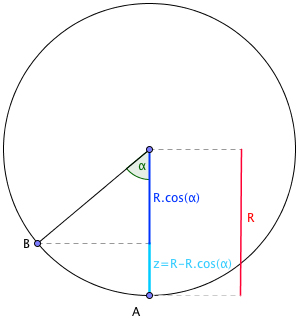
2. La première chose à faire est de représenter la situation avec un schéma ! Tu dois écrire différemment . Dans la boucle, quelle est la grandeur qui varie ? La masse (m) ? L'accélération de la pesanteur (g) ? Ou bien l'altitude (z) ? Je crois bien que c'est l'altitude !
Il faut donc que tu exprimes z en fonction de R et . Avec un schéma et un peu de trigo, pas trop de soucis (Voir mon schéma) ! Au final, tu peux donc écrire que
3. Ca, c'est une propriété de ton cours 
Toutes les forces en présence sont conservatives, l'énergie mécanique se conserve
4. a. Il faut utiliser le Théorème de l'énergie cinétique : . Le poids est la seule force qui travaille, tu peux donc écrire que
. Comme tu veux la vitesse en A, tu isoles
, ce qui te donnes :
b. Je te laisses faire l'application numérique
Merci pour l'aide !
Pour la 4), j'arrive bien à isoler VA seulement comment je fais l'application numérique vu que je ne connais pas la mesure de l'angle ?
Si ! Tu la connais lorsque le palet est au sommet de la boucle. Au début de l'énoncé, il est indiqué "Le palet peut effectuer la boucle si sa vitesse au sommet est supérieure a gR". L'angle et la vitesse
non ? Je crois qu'il y a quelque chose que je saisis pas :SEn fait, B est un point situé sur le cercle, à n'importe quel endroit. Il est repéré par l'angle . Sur le schéma, je l'ai placé au hasard, pour éviter de faire un cas particulier.
Dans la dernière question, on te demande de calculer la vitesse que doit avoir le palet en A pour qu'il puisse faire un tour complet, sachant que le palet peut faire un tour complet si il a une vitesse supérieure à au somment.
La formule qu'on a trouvé fonctionne pour toute les valeurs de à partir du moment où on a la vitesse du palet lorsqu'il occupe cette position. Lorsque le palet est au sommet, tu es d'accord avec moi, l'angle est égal à
et on connait la vitesse qu'il doit avoir. A partir de ça, tu as tous les renseignements dont tu as besoin, tu peux donc calculer la vitesse minimale de
1)
Em = (1/2).m.VA²
2)
Em = (1/2).m.v² + mgR(1 - cos(alpha))
3)
Parce qu'il n'y a pas de force de frottement.
4)
a)
(1/2).m.v² + mgR(1 - cos(alpha)) = (1/2).m.VA²
v² + 2gR(1 - cos(alpha)) = VA²
v² = VA² - 2gR(1 - cos(alpha))
Et pour effectuer la boucle complète, il faut que avec alpha = Pi (palet en haut de la boucle), v >= racinecarrée(gR) (La racine carrée est "oubliée" dans l'énoncé)
v² >= gR
VA² - 2gR(1 - cos(Pi)) >= gR
VA² - 4gR >= gR
VA² >= 5gR
VA >= racinecarrée(5gR)
Vitesse minimale de lancé = racinecarrée(5gR)
b)
Si R = 1,5 m
Vitesse minimale de lancé = racinecarrée(5*9,8*1,5) = 8,6 m/s
-----
Sauf distraction. Vérifie.
Annuler
connectez vous