Inscription / Connexion Nouveau Sujet
Attraction aquatique
Voici l'énoncé :
Cette attraction est constitué d'une rampe dont le point de départ A est situé à une hauteur de 8 m au-dessus du sol.Les utilisateurs sont assis sur une boué et se laisse glisser le long de la rampe ou une fine pellicule d'eau assure une parfaite glisse.
Morgane assise sur une boué , se laisse glisser sans vitesse initiale le long de la rampe.Une pellicule d'eau assure une descente sans frottement sur la partie AB.La masse A de l'ensemble = boué +Morgane est égal à m = 60 Kg.On admet que le système S est équivalent à uns solide en translation.
H=8m g =9,8 N/Kg
1) Exprimer la valeur de la vitesse de l'ensemble S au point B en fonction des données de l'exercice .
2)Le long de la rampe BC il n'y a pas de pellicule d'eau et l'ensemble S remonte jusqu'au point jusqu'au point D avant de redescendre.Pourquoi S n'atteint pas le sommet en C ?
3)Sachant que l'ensemble S perd la moitié de son énergie mécanique à chaque passage sur la partie BD , determinez la hauteur h'
4)Calculer la vitesse avec laquelle l'ensemble S va repasser une seconde fois au point B.
5)Calculer le nombre de passage au point B avec que S ne s'arrête.(on suppose que pour une hauteur de moins de 20cm l'ensemble S reste immobile )
Je veux ici savoir si mes réponses sont justes :
1) En sachant que l'énergie mécanique est conservé en AB , et que donc Epp = Em ,j'ai trouvé v = √9,81 *8*60 /30 = 12.52
2) L'énergie cinétique n'est pas assez importante
3) Em(A) =Em(B)= 4708.8 J :
4708.8 J = 8 m donc 4708.8 /2 J= 4 m
4) Comme Em est divisé par 2 alors Ec (=Epp) est lui aussi divisé par 2 donc :
v = (4708/2)/30 = 8,85
5 ) Je fais un produit en croix :
En sachant que pour 4708 J le système S fait 8 m , alors pour 0,2 m il faut 117 J
Ainsi 4708/2=2354
2354/2 =1177
1177/2 =588.5
588.5/2 =294.25
294.25/2 =147.125
147.125/2=73.56
Le système va donc passer 10 fois puis qu'il ne faut pas oublier les aller-retours.
Bonjour,
Il manque les unités un peu partout !
K en physique c'est le degré kelvin et k c'est le symbole de kilo (facteur 1000).
A partir de 4) ça me semble faux...
1 - Vu qu'il n'y a pas de frottements dans la descente AB, toute l'énergie potentielle est convertie en énergie cinétique et donc :
mv2/2 = mgh
D'où l'on tire :
VB = 
(2gh)
2 - Il y a perte d'énergie cinétique par frottement sur la partie montante BC dont la glisse est mauvaise. Toute l'énergie cinétique ne peut donc pas être transformée en énergie potentielle et h' < h.
3 - La moitié de l'énergie cinétique accumulée en B est perdue par frottement dans la remontée en D et le reste est converti en énergie potentielle. On écrit donc :
mgh/2 = mgh'
d'où h' = h/2
4 - La moitié de l'énergie potentielle acquise en D est convertie en énergie cinétique.
On a donc :
mv2/2 = mgh'/2
VB = (gh') = (gh/2)
5 - Comme il n'y a pas de perte d'énergie sur les remontées côté BA, les points de remontée sur BC sont situés à h/2, h/4, h/8... jusqu'à ce que h/(2n) < 0,2 m.
Il y a donc 11 passages par le point B.
Je te laisse vérifier tes résultats.
Des questions ?
Merci beaucoup pour la réponse.Je ne comprends juste pas pourquoi l'énergie potentielle au point D est divisé par 2 .Est-ce le fait que le système S subit une nouvelle fois des frottements ,une première fois de B à D et ensuite une seconde fois de D à B ?
Bien vu ! C'est tout à fait ça...
J'espère que tu as pu retrouver tes résultats et/ou corriger les erreurs.
Bonjour jeanduhivre, neajD
Je me suis interessé aux jeux aquatiques de Morgane.
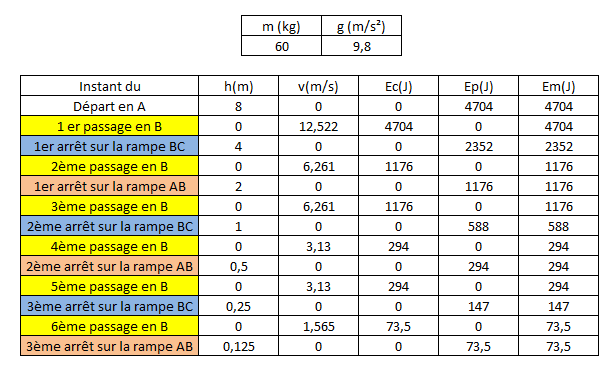
Bien que partageant vos analyses énergétiques je n'ai trouvé que 6 passages en B
Ci-dessous mes résultats sous forme de tableau.
Qu'en pensez vous ?
Bonjour,
Bien vu odbugt1 ! Comme quoi il faut toujours faire les calculs jusqu'au bout. Je m'étais dit simplement (bêtement ! 
) : On ne peut pas s'arrêter du côté AB puisqu'il n'y a pas de frottements. Comme jeanduhivre a trouvé 10 c'est donc 11 passages la bonne réponse. Par flemme, je n'avais fait aucun calcul.
Ceci dit, j'ai toujours un doute sur ta réponse odbugt1. Car mon hypothèse tient toujours et donc si j'étais jeanduhivre je répondrais 7 en justifiant cette réponse.
Cordialement.
Annuler
connectez vous