Inscription / Connexion Nouveau Sujet
Association de résistances.
Bonsoir,
J'aurais besoin d'un peu d'aide concernant un exercice de physique et précisément quant à sa compréhension.
L'énoncé est le suivant :
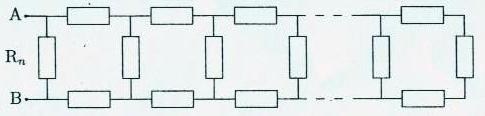
Tous les conducteurs ohmiques dessinés sur la première image jointe sont identiques, de résistance r. Soit R0 = r.
1. Calculer R1, R2 et R3, résistances équivalents des dipôles AB ainsi constitués.
2. Sur le même modèle que sur la deuxième image jointe, on construit le dipôle d'ordre n en mettant n structures identiques. Dessiner le dipôle n + 1 en faisant apparaître le dipôle n.
3. Montrer qu'on peut écrire Rn + 1 = r(2r + Rn) / (3r + Rn).
4. On suppose que quand n devient très grand, Rn tend vers une valeur constante appelée R
. Expliquer pourquoi R doit être solution de l'égalité suivante : R[/sub] = r(2r + R[sub]) / (3r + R).
5. Calculer R.
___________________________________________
Pour la question 1. je ne vois pas pourquoi on doit calculer R1, R2 et R3 si on nous dit que toutes les résistances sont identiques ?
Ou alors j'aurais mal compris la question ?
Merci d'avance de votre aide !
Bonsoir Seb 
Sur le deuxième schéma, les résistances sont en série, donc R1 = 3r.
Mais ce n'est que mon avis, l'énoncé n'est pas très clair 
Estelle 
Je comprends que R1 est la résistance équivalente aux trois autres mais elle n'est pas réellement dans le schéma, elle y est seulement représentée.
Mais ce n'est que mon interprétation
Estelle
Bonsoir Estelle,
En utilisant la formule de récurrence,R1=3r/4 et non 3r.
__.____.
| |
r r
| |
| r
| |
| r
| |
__.____.
donc 1/R1=1/r+1/3r=> R1=3r/4
La formule de récurrence ?
Est-ce au programme de première S parce que nous ne l'avons pas étudié...
Puis-je avoir des explications plutôt que des réponses seules s'il vous plait ?
Je souhaiterais comprendre l'exercice...
Merci !
Estelle>
3. Montrer qu'on peut écrire Rn + 1 = r(2r + Rn) / (3r + Rn).
Comment appelle t'on cette formule qui doit être valable pour:
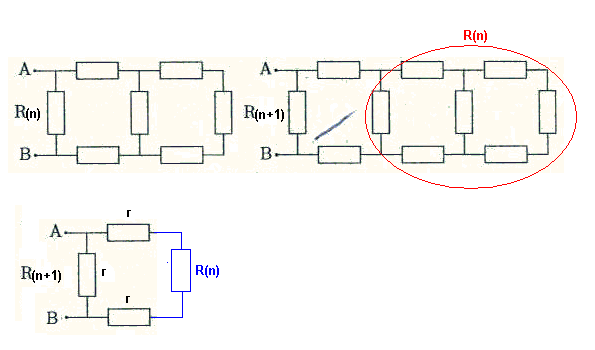
Il saute au yeux que :
R(n+1) = r en parallèle sur (2r + R(n))
-->
1/R(n+1) = 1/r + 1/(2r + R(n))
1/R(n+1) = [(2r + R(n)) + r]/[r.(2r + R(n))]
1/R(n+1) = (3r + R(n))/[r.(2r + R(n))]
R(n+1) = r.(2r + R(n))/(3r + R(n))
-----
Sauf distraction.
Le véritable dessin aurait dû être:
Calculer la résistance équivalente des dipôles AB que l'on notera:
R0,R1,R2,R3,...
et puis c'est pas Rn+1 qui est égal à Rinfini
c'est simplement une autre expression qui est valable lorsque n tend vers un grand nombre
4)
On suppose que quand n devient très grand, Rn tend vers une valeur constante appelée Roo
cela signifie que lim(n-> oo) R(n) = lim(n-> oo) R(n+1) = Roo
--> R(n+1) = r.(2r + R(n))/(3r + R(n))
lim(n-> oo) R(n+1) = lim(n-> oo) [ r.(2r + R(n))/(3r + R(n))]
Roo = r.(2r + Roo)/(3r + Roo)
-----
5)
Roo = r.(2r + Roo)/(3r + Roo)
Roo * (3r + Roo) = r.(2r + Roo)
3r.Roo + (Roo)² = 2r² + r.Roo
(Roo)² + 2r.Roo - 2r² = 0
Roo = -r +/- V(r² + 2r²) (Avec V pour racine carrée).
et comme Roo > 0 -->
Roo = r(V3 - 1)
-----
Sauf distraction.
Encore merci pour les explications.
J'ai presque terminé de rédiger cet exercice mais j'aimerais des détails concernant ce calcul :
(Roo)² + 2r.Roo - 2r² = 0
Roo = -r +/- V(r² + 2r²) (Avec V pour racine carrée).
Il faut une racine comme on a Roo au carré mais plus loin on a encore un Roo ; je ne comprends pas comment on passe à Roo = sa solution.
Merci d'avance !
(Roo)² + 2r.Roo - 2r² = 0
est une équation du second degré en Roo.
Il suffit donc de la résoudre par la manière qu'on t'a apprise.
Je connais la méthode avec le déterminant.
Je trouve :
a=1
b=2r
c=-2r²
delta = b²-4ac = (2r)²+8r²=12r²
Roo= -2r + V(12r²) / 2 = -r + V(6r²)
ou Roo= -2r - V(12r²) / 2 = -r - V(6r²)
Où est mon erreur ? merci.
Roo= (-2r + V(12r²)) / 2
Jusque là c'est OK mais pas plus loin ...
-----
Roo= (-2r + V(12r²)) / 2
Roo= (-2r/2) + (1/2).V(12r²)
Roo= -r + V(12r²/4)
Roo= -r + V(3r²)
Roo= -r + r.V3
Roo = r(V3 - 1)
-----
Annuler
connectez vous