Inscription / Connexion Nouveau Sujet
actions mécaniques(plan incliné)
Bonsoir à tous,
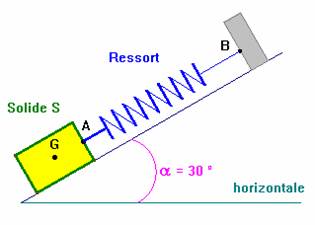
on considère un corps solide (s) de masse m=2kg, posé sans frottement sur un plan incliné faisant un angle 
= 30 degré avec l'horizontale.
le corps solide (s) est accroché par un ressort par l'intermédiaire d'un support.
1.Ecrire l'expression du poids du corps solide (s)dans le repère R(o,
) en fonction de m,g et .
2.sachant que le corps solide (s) a une forme géométrique cubique d'arête a=10cm.
2.1 ecrire l'expression littérale de la pression p exercée par le corps solide (s) sur le plan incliné en fonction de m,g,et a.
2.2 calculer sa valeur.
bon, je sais que : P=m.g , mais je ne sais pas comment introduire dans la relation.
Merci d'avance.
Il suffit de projeter le vecteur poids sur les axes et
. Si
est la "pente" du plan incliné et
l'axe perpendiculaire à la "pente", il faut utiliser les relations de trigonométrie dans un triangle rectangle...
Bonjour,
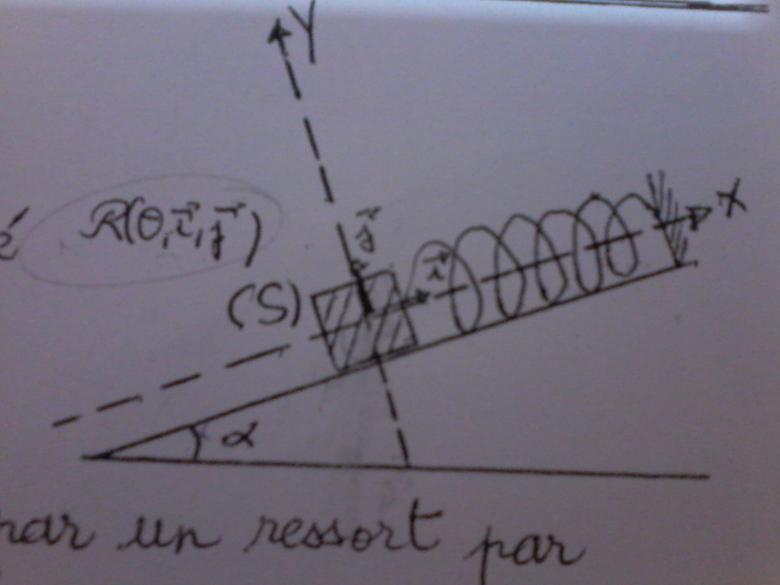
Où sont O,
et ?Ce n'est pas le même plan que j'ai, je n'ai pas su comment y insérer. J'essayerai.😅
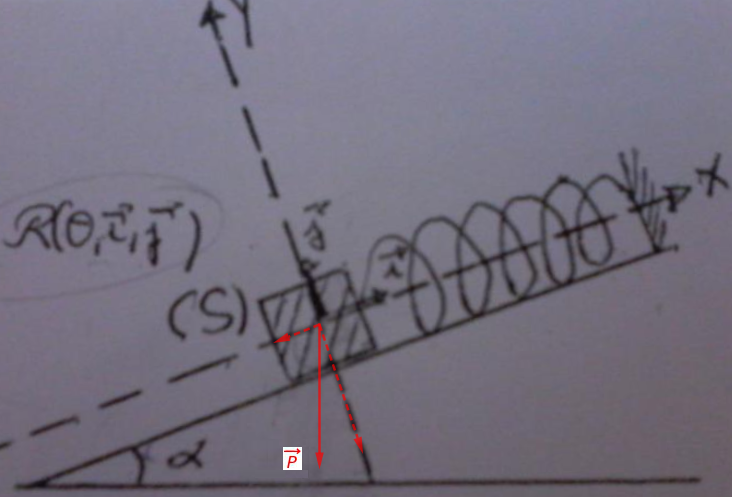
J'ai décomposé le vecteur en deux vecteurs
et
Voir figure.
de direction Ox, de sens opposé au vecteur unitaire
et de module P*sin(α)
de direction Oy, de sens opposé au vecteur unitaire
et de module P*cos(α)
D'où l'expression
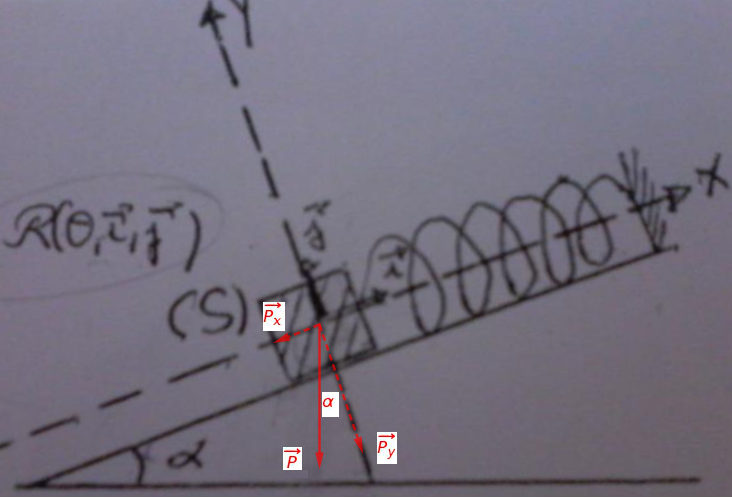
Voilà ce que j'ai fait:
1.la coordonné Px correspond à la projection du vecteur de la fore P sur l'axe des abscisses. (Px négative)
2.la coordonné Py correspond à la projection du vecteur de la force P sur l'axe des ordonnées. (Py négative)
Sin=-Py/||vecteur P||
D'où
x=sin×-||vecteur P||
Px=sin×(-P)
Cos=-Px/||vecteur P||
D'où: Py=cos ×-||vcteurP||
Py=cos×(-P)
(Py2+Px2)
Voilà ce que j'ai fait:
1.la coordonné Px correspond à la projection du vecteur de la fore P sur l'axe des abscisses. (Px négative)
2.la coordonné Py correspond à la projection du vecteur de la force P sur l'axe des ordonnées. (Py négative)
Sin
=-Py/||vecteur P||
D'où: Px=sin
×-||vecteur P||
Px=sin
×(-P)
Cos
=-Px/||vecteur P||
D'où: Py=cos
×-||vcteurP||
Py=cos
×(-P)Px et l'autre: Py
😅😅
Annuler
connectez vous