Inscription / Connexion Nouveau Sujet
2eme loi de Newton...
Bonjour,
Pourriez vous m'aider pour cet exercice sur un mobile autoporteur attaché à un ressort ...
Exercice:
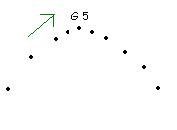
L'enregistrement ci dessous est celui du traceur central d'un mobile autoporteur attaché à un point fixe par un ressort et lancé sur une table horizontale.
La force exercée par le ressort est dans un plan parallèle à la table.
Période des impulsions  =40ms . échelle: 1/2
=40ms . échelle: 1/2
a) Dresser l'inventaire des forces qui s'exercent sur le mobile et montrer que l'ensemble se réduit à la force (vecteur) F exercée par le ressort.
b) Reproduire l'enregistrement et racer les vecteurs vitesse du centre d'Inertie du mobile aux points G 4 et G 6 en précisant l'échelle de représentation utilisée.
c) En déduire la direction et le sens de la force exercée par le ressort quand le centre d'Inertie passe par la position G 5.
d) Comment déterminer le point d'attache O du ressort ?
Merci 
Bonjour,
a) La table est horizontale donc la réaction du support et le poids se compensent totalement. La résultante des forces exercées sur le mobile Ftot = Rct + Pds + Fress est donc seulement égale à Fressort.
b) La valeur de la vitesse instantanée en un point donnée Gn est égale à la distance entre Gn+1 et Gn-1 divisée par le temps qui s'est écoulé entre ces deux points. C'est-à-dire le temps qu'il est lorsque le mobile est au point Gn+1 moins le temps qu'il était au point Gn-1.
En prenant G1 pour origine du repère: car entre chaque point il s'est écoulé une durée
 .
.
De même
La vitesse en mètres par seconde.
c) La force F, d'après la seconde loi de Newton est colinéaire et de même sens que l'accélération subit par le mobile. L'accélération en G5 se calcul en connaissant les vitesses en G4 et G6.
On a a5 = (v6-v4)/2*tau
Tu pourras en déduire la direction et le sens de F si tu traces le vecteur accélération instantanée .
d) La force F, exercée par le ressort, est une force de rappel qui tend à faire revenir le mobile vers le point d'attache du ressort en O. Connaissant la direction et le sens de la force F en plusieurs point G, tu peux par exemple tracer le point d'intersection des droites représentant les différentes directions de F.
pour répondre à tes questions
Gn+1 et Gn-1 sont les points correspondant à tes Mi+1 et Mi-1 dans la formule de calcul d'une vitesse instantanée
ton " tau" équivaut à une durée  .
.
Les mesures:
G1 à G2 = 1.2 cm
G2 à G3 = 0.7 cm
G3 à G4 = 0.6 cm
G4 à G5 = 0.5 cm
G5 à G6 = 0.4 cm
G6 à G7 = 0.3 cm
G7 à G8 = 0.7 cm
G8 à G9 = 0.8 cm
G9 à G10 = 0.8 cm
b) V4=G1G5 - G1 G3 / 2 x 40 x 10-3 = (2.7*10-2)-(1.8*10-2) / 80*10-3= 9*10-4/80*10-3 = 9*10-2*103 / 80 = 1.125*10-2
V6=G1G7 - G1G5 / 2*40*10-3= 0.031-0.027/ 80*10-3= 4*10-4*103/80 = 5*10-3
c) A5= (V6-V4)/2*40= (1.125*10-2)-(5*10-3)/80= 6.25*10-5/80=7.8125*10-7
Estce que les calculs sont bons?


