Inscription / Connexion Nouveau Sujet
Vitesse d'une boule de billard
Bonjour
C'est pour m'aider à faire un exercice,si vous pouvez me guider.
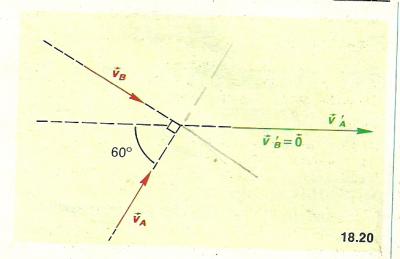
Deux boules de billard identiques , A et B , sont animés , dans un plan horizontal, d'un mouvement rectiligne et uniforme. Elles se heurtent à angle droit comme l'indique la figure ci-dessous. La vitesse de la boule A avant le choc est VA = 0,8m/s . Après le choc la vitesse de la boule B est nulle.
Calculer VB avant le choc et V'A après le choc. On admettra qu'il y a conservation de la quantité de mouvement.
Bonjour,
A priori, il faut écrire la conservation de la quantité de mouvement et la conservation de l'énergie cinétique.
Avec la conservation de la quantité de mouvement seule (même avec VB' = 0 (après le choc)), on a une équation à 2 inconnues VB et VA' donc ce n'est pas suffisant...
Bonjour,
Écris la conservation de la quantité de mouvement.
Tu auras ainsi deux équations à deux inconnues... et ce sera facile à résoudre !

Bonjour Aragorn 
Oups...
Mais, pour ma part, je n'ai pas eu besoin de prendre en compte l'énergie cinétique.

Il est indispensable de bien voir que ce ne sont pas des quantités scalaires mais que ce sont des vecteurs !
et ainsi tu vas pouvoir obtenir deux équations...

Ok merci, je vais les écrire en gras
Comment obtenir ces deux équations ?
VB = V'A - VA
V'A = VA - VB
Bonjour à tous.
VB = V'A - VA
V'A = VA - VB
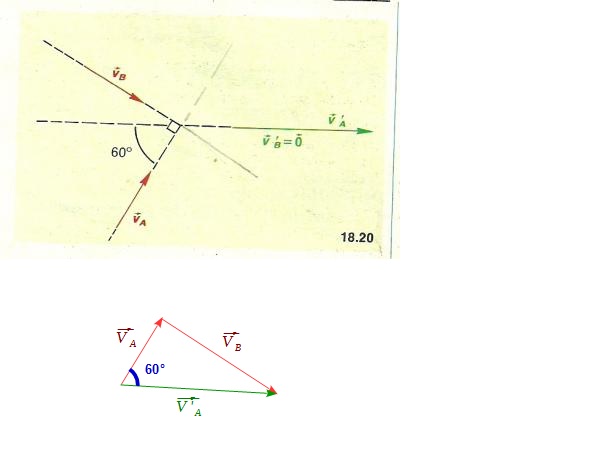
Sinon, tu peux aussi faire un schéma en plaçant
Tu as alors un triangle rectangle et tout est réglé en deux coups de trigo !
Au revoir.
Regarde la figure ci-dessous, en plaçant les vecteurs vitesse bout à bout, tu obtiens un triangle rectangle dans lequel tu connais VA et la valeur d'un des angles (et donc de tous...).
Avec deux relations de trigonométrie, tu peux déterminer VB et V'A.
OK ?
Si tu veux projeter, choisis tes axes pour avoir le moins possible de complications : un axe selon VA et l'autre selon VB ça peut être intéressant...
Mais la solution triangle rectangle (applicable ici mais pas dans n'importe quelle situation) est très intéressante.
A toi de voir.
Je veux projeter mais expliquer moi aussi avec le triangle rectangle.
En projetant je trouve
-VA -V'Acos30° = 0 (sur l'axe des x selon VA )
-VB -V'Acos60° = 0 (sur l'axe des y selon VB )
Je crois que ce que j'ai fait est faux.
En effet, c'est faux... Donc : recommence !
__________
La solution avec le triangle rectangle est d'autant plus "élégante" et facile que ce triangle rectangle est un demi-triangle équilatéral. Et donc que les relations entre les longueurs des côtés sont (devraient ? ... étaient autrefois...) connues par cœur.

Bon je trouve :
-VB+V'Acos30° = 0 ( l'axe x)
-VA+V'Acos60° = 0 (l'axe y)
Pouvez vous me montrer la solution en utilisant le triangle rectangle.
Quelles sont donc les valeurs de VB et de VA' ?
____________
Soit un triangle équilatéral ABC
H est le milieu de [AC]
Donc BH est hauteur, médiane, médiatrice, bissectrice...
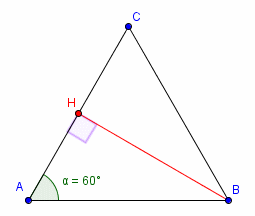
Si l'on note a la longueur commune aux côtés du triangle équilatéral (par exemple AB = a)
alors
et (par exemple, théorème de Pythagore)


 1,4 m.s-1
1,4 m.s-1

