Bonsoir
Tu trouveras ici une démonstration détaillée dans le cas de deux ressorts en série. Essaie de l'adapter à ton problème. Repose des questions précises si tu le juges utile en joignant un schéma du dispositif.

Bonsoir à vous deux,
Bienvenue à hibar sur notre forum,

Pour compléter la réponse de vanoise, on peut également évoquer ce sujet (clique sur la maison) : Ressorts équivalents à une association série et parallèle

Je vous laisse poursuivre,

Bonne soirée,

Bonjour,

Merci pour votre réponse et pour le document envoyé.
J'avoue avoir un peu de mal à l'adapter a mon problème.

J'arrive à exprimer les efforts mais je ne vois pas de quelle force et de quelle raideur (ou raideur équivalente) dépendent le déplacement aux point A et B ...

Y a-t-il une masse en B  ? Si non : le problème est très simple. Les 2 ressorts de droite peuvent être remplacés par un seul de raideur ke . L'expression de ke  correspond à l'association de 2 ressorts en série comme démontré sur le document.
Ensuite, vu de A, le ressort de raideur k1  et le ressort de raideur ke  sont équivalents à un seul ressort de raideur ke +k1. La démonstration correspond au paragraphe 2 du document.

Non, il n'y a aucune masse dans ce problème, ni en A ni en B. Juste une force connue appliquée en A.

Donc cela voudrait dire que la raideur équivalente de mon système est :

         K_eq = K₁ + k_e    avec    k_e = K₂.K₃/(K₁+K₂)  ? Même si les 3 ressorts sont en série ?

Mes déplacements au points A et B seraient alors :

        u_A = F / K_eq   ?
        u_B =  F_2/3 / K_eq   ?

Pour déterminer F_2/3, comment devrais-je procéder ?
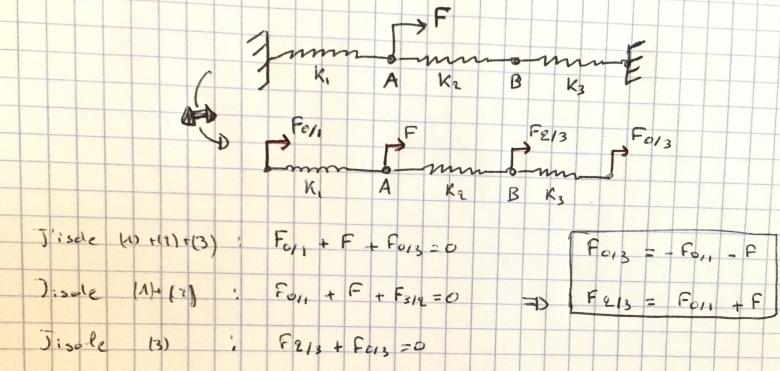
On m'a donné une piste qui consisterai à décomposer les efforts appliqués sur le système (par superposition) et à considérer les encastrements comme des efforts extérieurs (comme le 1e schéma).

Les 2 ressorts de droite sont en série.  Cette association est en parallèle avec le ressort de gauche car il y a  deux supports fixes comme au paragraphe 2 du document.
Su on note U _A le déplacement du point A, les trois ressorts exercent en A  la force -k.U_A avec :
k=k1+k2. k3/(k2+k3)
Si cela est utile, il est possible d'exprimer U_B en fonction de U_A en considérant que la tension se conserve le long des deux ressorts de droite  ( voir document ).
Difficile d'en dire plus sans avoir l'énoncé complet...

Ce n'est pas un énoncé complètement rédigé que j'ai ...

L'objectif est de trouver le déplacement d'une poutre sur appuis élastiques et soumise à une force F_A.

On assimile pour cela la poutre à un ressort de raideur K₂ = ES/L.

On se retrouve donc avec le système à 3 ressorts envoyé.

Je comprends mieux. Je pensais à l'étude d'un oscillateur...
Cependant, ma réponse de 23h04 me semble compatible avec ton dispositif.

Bonjour à vous deux,