Inscription / Connexion Nouveau Sujet
Ressorts équivalents à une association série et parallèle
Bonjour,
Pouvez-vous m'indiquer la méthode pour déterminer le ressort équivalent à une association série ou parallèle de ressort ?
Merci 
Skops 
Boa tarde Skops
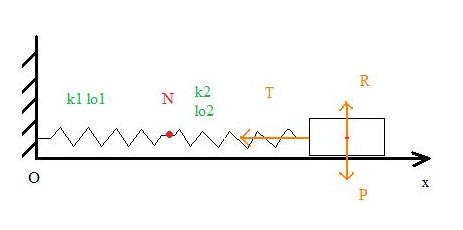
Considérons deux ressorts en parallèle.
* Système : {m}
* Référentiel : le sol, reférentiel terrestre supposé galiléen.
* Bilan des forces :
- le poids de {m}
- les forces de rappels exercées par les ressorts.
* D'après le principe fondamental de la dynamique en projection sur (Ox) on a :
(1)
* A l'équilibre, (2)
<=>
(1) - (2) =>
<=>
On pose X = (x-xe)
On a
Le système est équivalent à un unique ressort de raideur k=k1+k2.
Sauf erreur
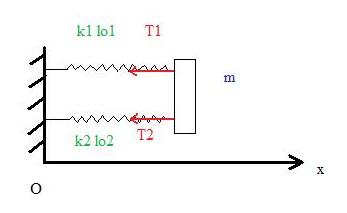
* D'après le principe fondamental de la dynamique en projection sur (Ox) on a :
m= -k2(l2-lo2)
on a x= l1(t)+l2(t)
* Soit N un point entre les deux ressorts.
M est la point d'application de la force de rappel .
On a donc m= -k2(xM - xN -lo2) (1)
* PFD sur N, mN=
+
en projection sur (Ox) on a 0 = -k1(xN - lo1) + k2(xM - xN - lo2) (2)
* A l'équilibre,
(1) => 0 = -k2(xMe - xNe -lo2) (3)
(2) => 0 = -k1(xNe - lo1) + k2(xMe - xNe - lo2) (4)
On a lo2 = xMe - xNe et d'après (2), xNe = lo1
Donc xMe = lo1 + lo2
* (1)-(3) => m = -k2(xM-xMe -(xN-xNe)).
(2)-(4) => 0 = -k1(xN-xMe) + k2(xM-xMe -(xN-xNe))
En posant XM = xM - xMe et XN = xN - xNe on a
m = -k2(XM - XN)
et
0 = -k1XN + k2(XM-XN)
XN = XM
donc m = -k2XM +
XM
soit
Le système est équivalent à un ressort 1/k = 1/k1 + 1/k2
Sauf erreur
Até breve 
Certes mais quand en DS, faut le redémontrer, c'est pas pareil 
l'inverse qu'en électricité ? taratata, il y a le même problème pour le condensateur
Skops
Ah oui en DS c'est une autre histoire
Si si, si on fait l'analogie : constante de raideur k <---------> résistance R 
Avec un peu de pipeau : "On a trivialement avec le PFD"
Avec un peu de culot : "C'est un ramassis d'évidence enfin"
Skops
Je sais qu'il n'y a pas de question con mais pardonnez mon ignorance : qu'est ce que signifie l'abréviation PDF ?!
pour les ressorts en série il ya une erreur sur le passage (4)-(2)
en effet il y a écrit (2)-(4) => 0 = -k1(xN-xMe) + k2(xM-xMe -(xN-xNe)) or une petite erreur de lettre s'est glissée en effet il faut écrire
(2)-(4) => 0 = -k1(xN-xNe) + k2(xM-xMe -(xN-xNe)) l'eereur est qu'il faut écrire Ne et non Me pour le premier terme
amicalement
Salut Folco,
Merci pour ces précisions.
Ca ne m'étonne pas, dans ces calculs à rallonge que j'ai fait une faute d'inattention.
Du moment que la méthode est comprise, c'est l'essentiel.
salut gbm,
tout à fait d'accord avec toi mais ayant vue l'erreur je me suis dis autant la corrigé pour d'autres, même si le topic date de 3 ans
une suite interessante de ce probleme serait se faire une analogie avec le théorème de Hooke, enfin ceci n'est pas le sujet ici )
Oui, en effet, mais là on vire limite dans le hors-programme, quoiqu'ils seraient capable de faire ça le jour du concours dans un problème.
Bonjour tout le monde!
Si on peut dire que l'équation (2) est nulle c'est parce qu'on considère que la masse du point N est nulle ?
Merci
Bonjour,
Veuillez me pardonner pour le déterrage mais je ne comprends pas bien l'équation (2) des ressorts en série :
en projection sur (Ox) on a 0 = -k1(xN - lo1) + k2(xM - xN - lo2) (2)
Pourquoi en N T2 change de sens par rapport en M ?
Hello
Pourquoi en N T2 change de sens par rapport en M ?
Parce que si en M, c'est la force
Avec la définition donnée de
M est la point d'application de la force de rappel
Il aurait fallu écrire en N:
* PFD sur N,
Par contre les projections sur l'axe Ox sont correctes ce qui est l'essentiel:
En M, si xM-xN > lo2 la mesure algébrique est bien -k2(xM - xN -lo2)
En N, si xM-xN > lo2 la mesure algébrique est bien +k2(xM - xN -lo2)
(nous remettrons cette minuscule coquille à sa place en re-enterrant le sujet
)
PS: j'en profite pour adresser à Gbm mes meilleurs voeux ainsi que l'assurance de mes indéfectibles confiance et admiration
Autrement :
Soit une force F appliquée à 2 ressorts de constante k1 et k2 en parallèle et dont l'ensemble varie de Delta L.
Chacun des ressorts subit ce même Delta L, soit F1 la force appliquée au ressort 1 et F2 la force appliquée au ressort 2.
F = F1 + F2
F1 = k1.Delta L
F2 = k2.Delta L
F = k1.Delta L + k2.Delta L
F = (k1+k2).Delta L
On a donc un ressort équivalent de constante (k1 + k2)
------------------
Soit une force F appliquée à 2 ressorts de constante k1 et k2 en série, soit delta L la variation de longueur totale.
Les 2 ressorts sont soumis à la même force -->
F1 = F2 = F
F1 = k1.Delta L1
F2 = k2.Delta L2
Delta 1 = F1/k1 = F/k1
Delta 2 = F1/k2 = F/k2
Et Delta L = Delta L1 + Delta L2 -->
Delta L = F/k1 + F/k2
Delta L = F * (1/k1 + 1/k2)
F = [1/(1/k1 + 1/k2)].Delta L
La constante élastique du ressort équivalent est : k = [1/(1/k1 + 1/k2)]
On a donc 1/k = 1/k1 + 1/k2
-----
Sauf distraction.
Bonjour à tous
Les 2 ressorts sont soumis à la même force -->
F1 = F2 = F
Cela peut effectivement s'admettre mais cela peut aussi simplement se démontrer. On peut aussi démontrer que la tension du ressort a même intensité à chacune de ses extrémités. Tout dépend du niveau où le problème est posé et de la rigueur exigée.
Je pense qu'une démonstration simple passe par l'application du principe des actions réciproques (action et réaction). Cela évite de donner à N une masse mN que l'on fait tendre ensuite vers zéro.
J'ai eu il y a quelques temps l'occasion de faire la démonstration sur ce forum :
Ressort en série Bonjour,
Je ne vois pas pourquoi en N vect(T1)=-vect(T2) avec vect(T1) le vecteur T1. En effet, lorsqu'on tire sur le ressorts 2 ; le 1 comme le 2 manifestent une résistance opposé au sens de traction. Donc en N on devrait avoir vect(T1)=+vect(T2). Qu'est ce qui ne va pas dans mon raisonnement ?
Dans l'explication de vanoise je ne comprends pas pourquoi vect(F) est à prendre en compte dans la deuxième loi de newton car une fois le ressort lâché (quand t=0) il n'intervient plus. Peux-tu m'éclairer ?
Dans l'explication de vanoise je ne comprends pas pourquoi vect(F) est à prendre en compte
Mais toutes les démonstrations supposent l'existence d'une action extérieure qui modifie la longueur de l'ensemble des deux ressorts : comme JP, je l'ai notée F ; sur le schéma proposé par gbm dans son message du 18-04-09 à 16:23, il s'agit de l'opposé de la force T exercé par le ressort sur la masse (ne pas oublier le principe des actions réciproques).
Mon schéma ne précise pas le système qui exerce la force F pour plus de généralité mais ce système existe nécessairement, sinon la loi de Hook sur la proportionnalité entre l'intensité de la force exercée par le ressort et son allongement ne s'appliquerait pas, il n'y aurait plus de raison de déterminer une raideur équivalente !
Ta question est tout de même très intéressante. Suppose effectivement un ressort (ou un ensemble de plusieurs ressorts en série) fixé à son extrémité supérieure à une potence fixe et tendue verticalement par un manipulateur. Celui-ci lâche le ressort de sorte que F =0. Que se passe-t-il ? L'étude n'a plus rien à voir avec ce qui a été écrit précédemment et relève de la mécanique des ondes : le phénomène se décrit comme la propagation d'une onde longitudinale le long du ressort, au moins si la déformation du ressort n'est pas trop importante. Sinon, il y a à la fois onde longitudinale et onde transversale...
PS : les lois de Newton en physique sont effectivement nettement supérieures à deux , à trois aussi d'ailleurs !
Salut à tous,
C'est de la statique des solides. Pour t'en convaincre, isole chacun des deux ressorts, tu verras qu'ils sont soumis à deux glisseurs forces .
Pense également au principe des actions réciproques.
PS: j'en profite pour adresser à Gbm mes meilleurs voeux ainsi que l'assurance de mes indéfectibles confiance et admiration
Merci dirac
! A mon tour de te souhaiter une très bonne année 2017 ainsi qu'aux autres membres ! Que mes meilleurs voeux vous accompagnent pour les 12 mois à venir !
Bonjour gbm
C'est de la statique des solides
Pas entièrement d'accord : dans la mesure où les masses des ressorts sont d'influence négligeable, les lois écrites précédemment sont aussi valides en dynamique et bien entendu, le principe des actions réciproques est valide dans tous les cas !
Bonsoir vanoise,
Oui bien entendu, j'essaie juste de simplifier le problème à un cas particulier, peut-être plus simple aux yeux de notre membre .
Cela reste effectivement tout aussi valide dans le cas général qu'est la dynamique.
Tout dépend du but recherché.
Soit on a à faire à un novice (non péjoratif) et on aborde le problème par des quasi évidences accessibles à tous pour autant qu'ils aient un minimum d'esprit physique.
... et on répond comme je l'ai fait.
Ou on à faire à des pros ... qui alors ne poseront pas une telle question. (je parle du post initial)
Je pense que trop souvent on s'embarque dans des démos bien trop sophistiquées par rapport à la question posée. Le mieux est très souvent l'ennemi du bien.
Mais cela n'engage que moi.
Bonjour
, gbm le mien c'est 2 ressorts verticaux ou on a entre les 2 une masse m Je remplace les deux ressorts par le ressort équivalent. Son allongement à l'équilibre, noté , vérifie :
En choisissant un axe (Ox) orienté vers le bas avec pour origine O, la position d'équilibre du centre d'inertie de la masse m, on remarque que, au cours du temps l'allongement est . La relation fondamentale de la dynamique appliquée au solide de masse m devient, en projection sur l'axe (Ox) :
On simplifie en tenant compte de la relation d'équilibre. Je te laisse conclure.
Tu as tout intérêt je crois à retenir qu'il est souvent simple d'étudier pour commencer la condition d'équilibre puis de prendre pour origine du repère la position d'équilibre...
je l'ai fait autrement avec des relations vectorielles et tout mais apres avoir gagne de l'experience en ressort je crois que je vais poster une fiche sur ces satanes ressorts
Et si la masse est a l'extremite verticale des 2 ressorts ?
Tu veux parler du cas 3 de la fiche que je t'ai indiquée ? Tu vas voir, c'est un peu plus délicat...
ke=(k1.k2)(k2+k1) n'est ce pas apres je remplace dans la formule magique que tu m'as donnee ?
vanoise si cette formule magique que tu as donnee est generale et il faut juste remplacer ke par son expression la alors c'est le paradis
Attention : pour les ressorts en série, ke est égal au produit des deux constantes divisé par leur somme et non l'inverse. Le reste du raisonnement est inchangé.
Jai le droit de l'ecrire comme t'as fait ici dur ma copie ?
Je remplace les deux ressorts par le ressort équivalent. Son allongement à l'équilibre, noté
En choisissant un axe (Ox) orienté vers le bas avec pour origine O, la position d'équilibre du centre d'inertie de la masse m, on remarque que, au cours du temps l'allongement est
On simplifie en tenant compte de la relation d'équilibre. Je te laisse conclure.
Tu as tout intérêt je crois à retenir qu'il est souvent simple d'étudier pour commencer la condition d'équilibre puis de prendre pour origine du repère la position d'équilibre...
Annuler
connectez vous